转载声明:文章来源https://blog.csdn.net/m0_73569204/article/details/135609132
4 二叉树、树和森林
重点章节,在选择,填空,综合中都有考察到。
4.1 掌握二叉树、树和森林的定义以及它们之间的异同点
1. 二叉树(Binary Tree)
定义: 二叉树是一种特殊的树结构,其中每个节点最多有两个子节点,通常称为左子节点和右子节点。这两个子节点的位置是有序的,左子节点的值小于或等于父节点的值,右子节点的值大于父节点的值。
特点:
- 每个节点最多有两个子节点。
- 子节点的位置有序,左子节点值 <= 父节点值,右子节点值 > 父节点值。
性质:
- 在二叉树的第i层上至多有2^(i-1)个结点(i>=1)。
- 深度为k的二叉树至多有2^k-1个结点(k>=1)。
- 对于任何一颗二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1。
- 具有n个节点的完全二叉树深为log2x+1(其中x表示不大于n的最大整数)。
- 如果对一颗有n个结点的完全二叉树(其深度为[log2n]+1)的结点按层序编号(从第一层到[log2n]+1层,每层从左到右),对任一结点i(1<=i<=n):
(1)如果i=1,则结点i是二叉树的根,无双亲,如果i>1,则其双亲结点是结点[i/2]
(2)如果2i>n,则结点i无左孩子(结点i为叶子结点)否则左孩子是结点2i。
(3)如果2i+1>n,则结点i无右孩子,否则其右孩子是结点2i+1.
2. 树(Tree)
定义: 树是一种层次结构的数据结构,由节点和连接这些节点的边组成。树中有一个特殊的节点称为根节点,除了根节点之外,每个节点有且只有一个父节点,但可以有多个子节点。
特点:
- 每个节点有且只有一个父节点,除了根节点。
- 节点之间通过边相连,形成层次结构。
3. 森林(Forest)
定义: 森林是多个独立的树组成的集合。每个树都是独立的,没有公共的根节点。换句话说,森林是多个树的集合。
特点:
- 由多个独立的树组成。
- 每个树都是独立的,没有公共的根节点。
异同点
1节点数量:
- 二叉树:每个节点最多有两个子节点。
- 树:每个节点有且只有一个父节点。
- 森林:由多个独立的树组成。
2连接关系:
- 二叉树:每个节点有左子节点和右子节点。
- 树:除了根节点,每个节点有一个父节点。
- 森林:独立的树结构,没有公共的根节点。
3结构关系:
- 二叉树和树是单一的结构。
- 森林是由多个独立的树组成的集合。
总体上,可以看出树是一种更一般的结构,而二叉树是树的一种特殊情况。森林是由多个树组成的结构。
4.2 掌握二叉树的四种遍历,并具有能够依赖遍历完成对二叉树进行操作的能力
期末试卷中填空题考到了根据给出的先序遍历和中序遍历字符串写出后序遍历的字符串。
二叉树的四种遍历方式包括前序遍历、中序遍历、后序遍历和层序遍历。可视化网站:Binary Tree Traversal
1. 前序遍历(Preorder Traversal):
前序遍历的顺序是先访问根节点,然后递归地进行左子树的前序遍历,最后递归地进行右子树的前序遍历。
根 -> 左子树 -> 右子树class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public class BinaryTreeTraversal {
public static void preorderTraversal(TreeNode root) {
if (root != null) {
System.out.print(root.val + " ");
preorderTraversal(root.left);
preorderTraversal(root.right);
}
}
public static void main(String[] args) {
// 构建一棵二叉树
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
// 前序遍历
System.out.println("Preorder Traversal:");
preorderTraversal(root);
}
}
2. 中序遍历(Inorder Traversal)
中序遍历的顺序是先递归地进行左子树的中序遍历,然后访问根节点,最后递归地进行右子树的中序遍历。
左子树 -> 根 -> 右子树class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public class BinaryTreeTraversal {
public static void inorderTraversal(TreeNode root) {
if (root != null) {
inorderTraversal(root.left);
System.out.print(root.val + " ");
inorderTraversal(root.right);
}
}
public static void main(String[] args) {
// 构建一棵二叉树
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
// 中序遍历
System.out.println("Inorder Traversal:");
inorderTraversal(root);
}
}
3. 后序遍历(Postorder Traversal)
后序遍历的顺序是先递归地进行左子树的后序遍历,然后递归地进行右子树的后序遍历,最后访问根节点。
左子树 -> 右子树 -> 根class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public class BinaryTreeTraversal {
public static void postorderTraversal(TreeNode root) {
if (root != null) {
postorderTraversal(root.left);
postorderTraversal(root.right);
System.out.print(root.val + " ");
}
}
public static void main(String[] args) {
// 构建一棵二叉树
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
// 后序遍历
System.out.println("Postorder Traversal:");
postorderTraversal(root);
}
}
4. 层序遍历(Level Order Traversal)
层序遍历按照层次逐层遍历二叉树,从根节点开始,每一层按照从左到右的顺序访问节点。
import java.util.LinkedList;
import java.util.Queue;
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public class BinaryTreeTraversal {
public static void levelOrderTraversal(TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode current = queue.poll();
System.out.print(current.val + " ");
if (current.left != null) {
queue.offer(current.left);
}
if (current.right != null) {
queue.offer(current.right);
}
}
}
public static void main(String[] args) {
// 构建一棵二叉树
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
// 层序遍历
System.out.println("Level Order Traversal:");
levelOrderTraversal(root);
}
}这些遍历方式可以用于对二叉树进行不同类型的操作,例如查找节点、计算树的深度等。
4.3 理解二叉树采用顺序存储结构和链式存储结构的差异性
二叉树可以使用两种不同的存储结构:顺序存储结构和链式存储结构。
1. 顺序存储结构
在顺序存储结构中,使用数组来表示二叉树的节点。二叉树的节点按照某种顺序存储在数组中,可以根据节点在数组中的位置快速找到其父节点、左子节点和右子节点。
特点:
- 使用数组作为存储结构。
- 通过数组下标关系表示节点之间的层次和父子关系。
- 不需要额外的指针,节省存储空间。
缺点:
- 对于非完全二叉树,可能浪费一些数组空间。
- 插入和删除节点操作可能需要移动其他节点,效率较低。
2. 链式存储结构
在链式存储结构中,通过使用节点对象和指针,将节点按照树的层次关系连接在一起。每个节点包含数据和指向左右子节点的指针。
特点:
- 使用节点对象和指针来表示节点之间的关系。
- 可以方便地插入和删除节点,不需要移动其他节点。
- 适用于不规则的树结构,不会浪费空间。
缺点:
- 每个节点需要额外的指针空间,占用更多的存储空间。
- 对于大规模数据的二叉树,可能存在指针的空间开销。
差异性比较
1存储结构:
- 顺序存储结构使用数组。
- 链式存储结构使用节点对象和指针。
2存储方式:
- 顺序存储结构通过数组下标表示节点关系。
- 链式存储结构通过指针连接节点。
3空间效率:
- 顺序存储结构可能浪费一些空间,特别是对于非完全二叉树。
- 链式存储结构对于不规则的树结构更灵活,不会浪费空间。
4时间效率:
- 顺序存储结构的插入和删除操作可能需要移动其他节点,效率较低。
- 链式存储结构对于插入和删除操作更灵活,效率较高。
选择使用哪种存储结构取决于具体应用场景和需求。如果二叉树的结构较规则且不频繁发生变化,顺序存储结构可能更为合适。如果二叉树结构较为灵活且需要频繁插入和删除操作,链式存储结构可能更适用。
4.4 掌握二叉检索树、Huffman编码以及堆的实现
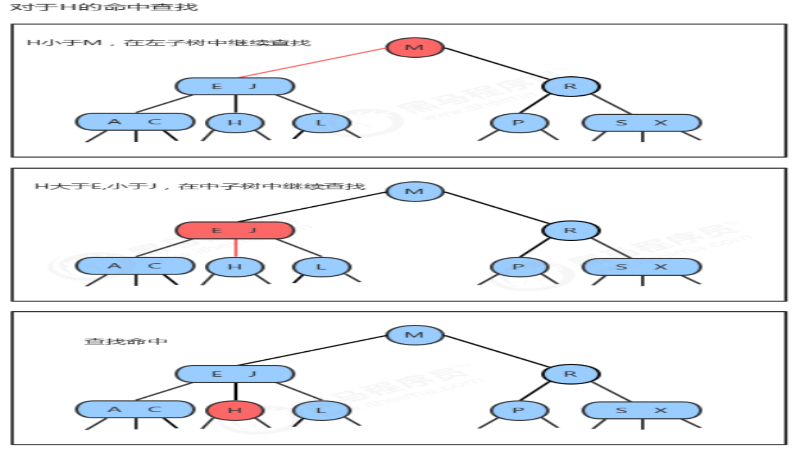
1. 二叉搜索树(Binary Search Tree,BST)
定义: 二叉搜索树是一种二叉树,其中每个节点的值大于其左子树中的所有节点的值,且小于其右子树中的所有节点的值。
实现要点:
- 节点的左子树的所有节点值都小于节点的值。
- 节点的右子树的所有节点值都大于节点的值。
- 左右子树也分别是二叉搜索树。
Java 代码示例:
class TreeNode {
int val;
TreeNode left, right;
public TreeNode(int val) {
this.val = val;
this.left = this.right = null;
}
}
public class BinarySearchTree {
private TreeNode root;
// 插入节点
public void insert(int key) {
root = insertRec(root, key);
}
private TreeNode insertRec(TreeNode root, int key) {
if (root == null) {
root = new TreeNode(key);
return root;
}
if (key < root.val) {
root.left = insertRec(root.left, key);
} else if (key > root.val) {
root.right = insertRec(root.right, key);
}
return root;
}
// 中序遍历
public void inorder() {
inorderRec(root);
}
private void inorderRec(TreeNode root) {
if (root != null) {
inorderRec(root.left);
System.out.print(root.val + " ");
inorderRec(root.right);
}
}
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
int[] keys = {50, 30, 20, 40, 70, 60, 80};
for (int key : keys) {
bst.insert(key);
}
System.out.println("Inorder traversal:");
bst.inorder();
}
}2. Huffman 编码
定义: Huffman 编码是一种压缩算法,通过构建最优二叉树(Huffman 树)来实现对数据的压缩。频率越高的字符对应的编码越短,频率越低的字符对应的编码越长。
实现要点:
- 构建 Huffman 树。
- 通过 Huffman 树生成字符的编码。
Java 代码示例:
import java.util.PriorityQueue;
class HuffmanNode implements Comparable<HuffmanNode> {
char data;
int frequency;
HuffmanNode left, right;
public HuffmanNode(char data, int frequency) {
this.data = data;
this.frequency = frequency;
this.left = this.right = null;
}
@Override
public int compareTo(HuffmanNode node) {
return this.frequency - node.frequency;
}
}
public class HuffmanCoding {
public static void main(String[] args) {
String input = "hello world";
// 构建 Huffman 树
HuffmanNode root = buildHuffmanTree(input);
// 生成 Huffman 编码
System.out.println("Huffman Codes:");
printHuffmanCodes(root, new StringBuilder());
}
private static HuffmanNode buildHuffmanTree(String input) {
// 统计字符频率
int[] frequency = new int[256];
for (char ch : input.toCharArray()) {
frequency[ch]++;
}
// 构建最小堆(PriorityQueue)
PriorityQueue<HuffmanNode> minHeap = new PriorityQueue<>();
for (char i = 0; i < 256; i++) {
if (frequency[i] > 0) {
minHeap.offer(new HuffmanNode(i, frequency[i]));
}
}
// 构建 Huffman 树
while (minHeap.size() > 1) {
HuffmanNode left = minHeap.poll();
HuffmanNode right = minHeap.poll();
HuffmanNode internalNode = new HuffmanNode('$', left.frequency + right.frequency);
internalNode.left = left;
internalNode.right = right;
minHeap.offer(internalNode);
}
return minHeap.poll(); // 返回 Huffman 树的根节点
}
private static void printHuffmanCodes(HuffmanNode root, StringBuilder code) {
if (root == null) {
return;
}
// 叶子节点表示一个字符,打印字符和对应的 Huffman 编码
if (root.data != '$') {
System.out.println(root.data + ": " + code);
}
// 递归处理左子树
code.append('0');
printHuffmanCodes(root.left, code);
code.deleteCharAt(code.length() - 1);
// 递归处理右子树
code.append('1');
printHuffmanCodes(root.right, code);
code.deleteCharAt(code.length() - 1);
}
}3. 堆的实现
期末试卷中填空题考到了构建二叉检索树,涉及筛选法构建最小堆
定义: 堆是一种特殊的树状数据结构,其中每个节点的值都小于或等于其子节点的值。堆分为最大堆和最小堆。
实现要点:
- 最大堆:每个节点的值都大于或等于其子节点的值。
- 最小堆:每个节点的值都小于或等于其子节点的值。
- 堆的常见操作:插入节点、删除节点、堆化(维护堆的性质)。
Java 代码示例:
public class MaxHeap {
private int[] heap;
private int size;
private int capacity;
public MaxHeap(int capacity) {
this.capacity = capacity;
this.size = 0;
this.heap = new int[capacity + 1];
}
public void insert(int value) {
if (size == capacity) {
System.out.println("Heap is full. Cannot insert " + value);
return;
}
size++;
heap[size] = value;
int current = size;
// 上移操作,维护堆的性质
while (current > 1 && heap[current] > heap[parent(current)]) {
swap(current, parent(current));
current = parent(current);
}4.5 掌握树、森林采用的各种存储方式的差异性
期末试卷中综合题考察了树和森林的转换,要求用双亲表示法。
树的存储方式
1.双亲表示法:
在双亲表示法中,每个节点包含一个指向其父节点的指针,以及一个指向其第一个子节点的指针。通过这种方式,可以方便地找到父节点和第一个子节点。
class TreeNode {
int data;
int parent; // 父节点的索引
}
// 示例:树的双亲表示法
TreeNode[] tree = new TreeNode[10];2.孩子表示法:
在孩子表示法中,每个节点包含一个指向其第一个子节点的指针,以及一个指向其右兄弟节点的指针。这种表示法适用于节点的子节点数量不固定的情况。
class TreeNode {
int data;
TreeNode firstChild; // 指向第一个子节点
TreeNode nextSibling; // 指向右兄弟节点
}
// 示例:树的孩子表示法
TreeNode root = new TreeNode();森林的存储方式
森林是多棵树的集合。存储森林可以采用上述树的存储方式,每个树用一个独立的数据结构表示。
class ForestNode {
int data;
ForestNode firstChild; // 指向第一个子节点
ForestNode nextSibling; // 指向右兄弟节点
}
// 示例:森林的存储
ForestNode tree1 = new ForestNode();
ForestNode tree2 = new ForestNode();这里的 ForestNode 类似于树的孩子表示法,每个树用一个节点表示,节点的 firstChild 指向树的根节点,nextSibling 指向其他树的根节点。
4.6 掌握树和森林与二叉树的转换
1.树转换为二叉树
树到二叉树的转换可以通过以下步骤完成:
- 每个节点添加右兄弟指针: 对树的每个节点,将它的所有子节点按照从左到右的顺序连接起来,形成右兄弟链。
- 去除父节点指针: 去掉树的每个节点中指向父节点的指针。
- 添加二叉树的左右孩子指针: 对树的每个节点,将其第一个子节点作为二叉树的左孩子,将其右兄弟节点作为二叉树的右孩子。
class TreeNode {
int data;
TreeNode firstChild; // 指向第一个子节点
TreeNode nextSibling; // 指向右兄弟节点
}
class BinaryTreeNode {
int data;
BinaryTreeNode leftChild; // 左孩子
BinaryTreeNode rightChild; // 右孩子
}
public class TreeToBinaryTreeConverter {
public static BinaryTreeNode convertTreeToBinaryTree(TreeNode root) {
if (root == null) {
return null;
}
BinaryTreeNode binaryRoot = new BinaryTreeNode();
binaryRoot.data = root.data;
// 将树的子节点转换为二叉树的左孩子
binaryRoot.leftChild = convertTreeToBinaryTree(root.firstChild);
// 将树的右兄弟节点转换为二叉树的右孩子
binaryRoot.rightChild = convertTreeToBinaryTree(root.nextSibling);
return binaryRoot;
}
}二叉树转换为树:
二叉树到树的转换相对简单,只需将二叉树的右孩子链表还原为树的右兄弟链。
class BinaryTreeNode {
int data;
BinaryTreeNode leftChild; // 左孩子
BinaryTreeNode rightChild; // 右孩子
}
class TreeNode {
int data;
TreeNode firstChild; // 指向第一个子节点
TreeNode nextSibling; // 指向右兄弟节点
}
public class BinaryTreeToTreeConverter {
public static TreeNode convertBinaryTreeToTree(BinaryTreeNode binaryRoot) {
if (binaryRoot == null) {
return null;
}
TreeNode root = new TreeNode();
root.data = binaryRoot.data;
// 将二叉树的左孩子转换为树的第一个子节点
root.firstChild = convertBinaryTreeToTree(binaryRoot.leftChild);
// 将二叉树的右孩子转换为树的右兄弟节点
root.nextSibling = convertBinaryTreeToTree(binaryRoot.rightChild);
return root;
}
}4.7 掌握树、森林在遍历方面和二叉树的不同以及相关性
树的遍历
- 先序遍历(Preorder Traversal): 先访问根节点,然后递归地对每个子树进行先序遍历。
- 后序遍历(Postorder Traversal): 先递归地对每个子树进行后序遍历,然后访问根节点。
- 层次遍历: 从树的根节点开始,按层次逐层遍历。
森林的遍历
森林是多棵树的集合,因此森林的遍历就是对每棵树进行遍历。可以采用树的遍历方式。
二叉树的遍历
在二叉树中,有以下三种常见的遍历方式:
- 先序遍历(Preorder Traversal): 先访问根节点,然后递归地对左子树和右子树进行先序遍历。
- 中序遍历(Inorder Traversal): 先递归地对左子树进行中序遍历,然后访问根节点,最后递归地对右子树进行中序遍历。
- 后序遍历(Postorder Traversal): 先递归地对左子树和右子树进行后序遍历,然后访问根节点。
这三种遍历方式对于树、森林和二叉树都是适用的,但在树和森林的情况下,可能需要对每棵树分别进行遍历。
相关性和不同点
- 共同点: 树、森林和二叉树都可以使用先序、中序和后序等遍历方式。
- 不同点: 在树和森林中,节点的子节点数量不一定是固定的,因此在遍历时可能需要通过指向第一个子节点和右兄弟节点的方式进行遍历。而在二叉树中,每个节点最多有两个子节点,可以采用左孩子和右孩子的方式进行遍历。
下面是一个简单的 Java 代码示例,演示了树的先序遍历:
class TreeNode {
int data;
TreeNode firstChild; // 指向第一个子节点
TreeNode nextSibling; // 指向右兄弟节点
}
public class TreeTraversal {
// 先序遍历树
public static void preOrderTraversal(TreeNode root) {
if (root == null) {
return;
}
// 访问根节点
System.out.print(root.data + " ");
// 递归遍历子树
preOrderTraversal(root.firstChild);
// 递归遍历右兄弟节点
preOrderTraversal(root.nextSibling);
}
public static void main(String[] args) {
TreeNode root = new TreeNode();
root.data = 1;
TreeNode child1 = new TreeNode();
child1.data = 2;
TreeNode child2 = new TreeNode();
child2.data = 3;
root.firstChild = child1;
child1.nextSibling = child2;
preOrderTraversal(root);
}
}4.8 理解并查集的意义,掌握并查集两个基本操作的实现并掌握重量权衡平衡原则和路径压缩
并查集(Disjoint Set Union,简称并查集)是一种用于处理不相交集合的数据结构,主要用于解决一些集合合并与查询问题。它支持两个主要操作:查找(Find)和合并(Union)。
并查集的基本操作
- 查找(Find): 查找一个元素所属的集合,通常通过找到该集合的代表元素来实现。
- 合并(Union): 合并两个集合,通常将其中一个集合的代表元素作为另一个集合的子集。
实现并查集的两种基本方法
数组表示法: 将每个元素用数组表示,数组的值表示该元素所属的集合。parent[i] 表示元素 i 的父节点,根节点的父节点为自身。
int[] parent = new int[n];
// 初始化,每个元素独立成集合,父节点为自身
for (int i = 0; i < n; i++) {
parent[i] = i;
}
// 查找操作
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]); // 路径压缩
}
return parent[x];
}
// 合并操作
void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
parent[rootX] = rootY; // 合并时可以考虑根据集合大小进行重量权衡
}
}树表示法: 将每个集合表示为一棵树,其中树的根节点为代表元素。
class TreeNode {
int val;
TreeNode parent;
}
// 查找操作
TreeNode find(TreeNode x) {
if (x.parent != null) {
x.parent = find(x.parent); // 路径压缩
return x.parent;
}
return x;
}
// 合并操作
void union(TreeNode x, TreeNode y) {
TreeNode rootX = find(x);
TreeNode rootY = find(y);
if (rootX != rootY) {
rootX.parent = rootY; // 合并时可以考虑根据集合大小进行重量权衡
}
}重量权衡平衡原则
在合并操作时,可以考虑根据集合的大小进行重量权衡,即将元素较少的集合合并到元素较多的集合中,从而降低树的深度,提高效率。
路径压缩
在查找操作时,通过路径压缩可以将树的深度降低,使得后续查找操作更加高效。路径压缩的思想是在查找的同时,将查找路径上的节点直接连接到根节点,使得路径更短。



帖子还没人回复快来抢沙发