转载声明:文章来源https://blog.csdn.net/wwb44444/article/details/112986138
一、图的实现
图的实现主要有两种方式,一种是邻接矩阵,一种是邻接表。
所谓邻接矩阵就是构建一个节点到节点的矩阵,每一行每一列都代表一个节点,矩阵的输入数据即为该位置所在的行和列对应的节点之间是否可达。一般而言,若该数值为表示不可达,为一个正数表示该条边的权值。矩阵对角线上的数值一般为0,表示各个节点到其自身的距离,所以是0。当然,不考虑权值的情况(仅说明是否可达)一般矩阵的值为0和1,0表示不可达,1表示可达。邻接矩阵示意图如下:

如图矩阵中的6表示v0到v4的边权值为6。邻接矩阵的实现方式一般使用二维线性数组,与上图的矩阵一一对应,很好理解。
邻接表是基于链表思想的另一种实现方式,简单来说就是将图中各个顶点看做一种特殊的线性数组,数组的每个位置表示一个节点作为起点的所有相连边。考虑到一个节点可能有多个相连边,于是可将这些相连边以链表的方式全部存储到数组的该位置。是不是听起来有点像散列表?或者有点像HashMap?,不过它比HashMap简单多了,链表不会转化为红黑树,而且节点在数组中是线性存放的,不需要hash值,也不需要路由寻址。具体邻接表示意图如下:
如上图,1与2、3、5连接,2与1、4连接,这就是邻接表。本文所讲的图的遍历都是基于邻接表的,邻接矩阵同理,会更为简单一些。不过我所设计的邻接表中每一个节点并不像上图那么简单,而是包含三条信息:起始点,终点,权值。每个节点即代表一条边。下面我具体来谈谈实现原理。
邻接表在我看来就是数组加链表,数组中存放的数值为对应位置链表的第一个节点,同一位置的链表节点彼此相连,这就意味着数组有多长就会有多少个链表。
首先,需要定义链表节点类,类包含四个属性:起始点,终点,权值,指向下一节点的指针。
//边
public class Triple implements Comparable<Triple> {
int row, column, value; //行号(起点序号),列号(终点序号),元素(权值)
Triple next = null;
public Triple(int row, int column, int value) {
this.row = row;
this.column = column;
this.value = value;
}
//按行列位置比较三元组对象大小,约定排序次序
@Override
public int compareTo(Triple tri) {
return 0;
}
}这里的行号,列号是针对邻接矩阵来讲的,在邻接表中就是起始点序号和终点序号。
邻接表即为一个Triple对象数组Triple[]
public class AdjListGraph<T> extends AbstractGraph<T> {
protected Triple[] rowlist;除了邻接表数组外我们还需要一个存储节点的数组,这些我都定义在了抽象父类AbstractGraph中。
public abstract class AbstractGraph<T> implements Graph<T> {
protected static final int MAX_WEIGHT = 0x0000fffff; //最大权值(表示无穷大)
protected ArrayList<T> vertexlist; //顶点顺序表,存储图的顶点集合
public AbstractGraph() {
this.vertexlist = new ArrayList<T>();
}
//返回顶点数
@Override
public int vertexCount() {
return this.vertexlist.size();
}
//返回顶点vi元素
@Override
public T get(int i) {
return this.vertexlist.get(i);
}做好了这些准备工作,接下来就是初始化邻接表,往里插入顶点和边。我们选择构造函数完成上述操作。
public AdjListGraph(T[] vertexes, Triple[] edges){
int pointNum = vertexes.length; //顶点数量
vertexlist = new ArrayList<>(pointNum);
rowlist = new Triple[pointNum];
for(int i=0; i<pointNum; i++){
insertVertex(vertexes[i]); //插入顶点
}
for(int i=0; i<edges.length; i++){
insertEdge(edges[i]); //插入边
}
}这里构造函数的输入为一个点集和边集,根据顶点的数量初始化顶点数组和邻接表数组,并分别调用插入顶点和插入边的操作完成插入操作。
在主函数中给出了此处输入的点集和边集,读者不妨自己画出这张图。
//顶点集合
String[] vertexes = {"A", "B", "C", "D", "E", "F"};
//边集合
Triple[] edges = {new Triple(0, 1, 45), new Triple(0, 2, 28),
new Triple(0, 3, 10), new Triple(1, 0, 45),
new Triple(1, 2, 12), new Triple(1, 4, 21),
new Triple(2, 0, 28), new Triple(2, 1, 12),
new Triple(2, 3, 17), new Triple(2, 4, 26),
new Triple(3, 0, 10), new Triple(3, 2, 17),
new Triple(3, 4, 15), new Triple(3, 5, 13),
new Triple(4, 1, 21), new Triple(4, 3, 15),
new Triple(5, 3, 13), new Triple(5, 4, 11)};插入节点的操作很简单,就是往ArrayList中循环插点即可。
//插入顶点
public void insertVertex(T point){
if(point != null) {
vertexlist.add(point);
if(vertexlist.size() > rowlist.length){
resize(); //邻接表扩容
}
}
else
throw new IllegalArgumentException();
}
//邻接表扩容
private void resize(){
int newLength = rowlist.length * 2;
Triple[] newRowlist = new Triple[newLength];
for(int i=0; i<rowlist.length; i++){
newRowlist[i] = rowlist[i];
}
rowlist = newRowlist;
}不过,这里要考虑到在初始化顶点数组后,后续还可能继续插入新的顶点和边,则顶点数组和邻接表数组都需随之扩容,ArrayList有自己的扩容机制这里不再展开,仅对邻接表数组进行扩容,其逻辑即当顶点数组的容量超过了邻接表数组的容量(邻接表数组占用的内存空间全部使用完毕)触发扩容,扩容方式为构建一个新的邻接表数组,其容量是原数组容量的2倍,然后将其中的链表节点全部复制到新数组中,最后将新数组对象地址赋给rowlist。
插入边即构造链表。首先判断插入的边的起点、终点和权值是否合法,不合法则报错。在插入时存在两种情况,第一种情况为邻接表数组该位置为空,即尚未有任何边插入,则直接插入即可。第二种情况为插入位置不为空,表示已有节点(链表节点,下同),则循环遍历到链表尾并插入。
//插入边
public void insertEdge(Triple edge){
if(edge.row < rowlist.length && edge.column < rowlist.length && edge.value < MAX_WEIGHT){
if(rowlist[edge.row] == null){ //邻接表插入位置为空,直接插入
rowlist[edge.row] = edge;
}else{ //插入位置不为空,插入链表尾端
Triple node = rowlist[edge.row];
while(node.next != null){
node = node.next;
}
node.next = edge;
}
}else
throw new IllegalArgumentException();
}最后覆写toString方法作为输出之用。
public String toString(){
String str = super.toString() + "出边表:\n";
str += "起点\t\t终点\t\t权值\n";
for(int i=0; i<rowlist.length; i++){
if(rowlist[i] == null) continue;
Triple node = rowlist[i];
while(node != null){
str += node.row + "\t\t" + node.column + "\t\t" + node.value + "\n";
node = node.next;
}
}
return str;
}输出结果如下:

二、深度优先遍历
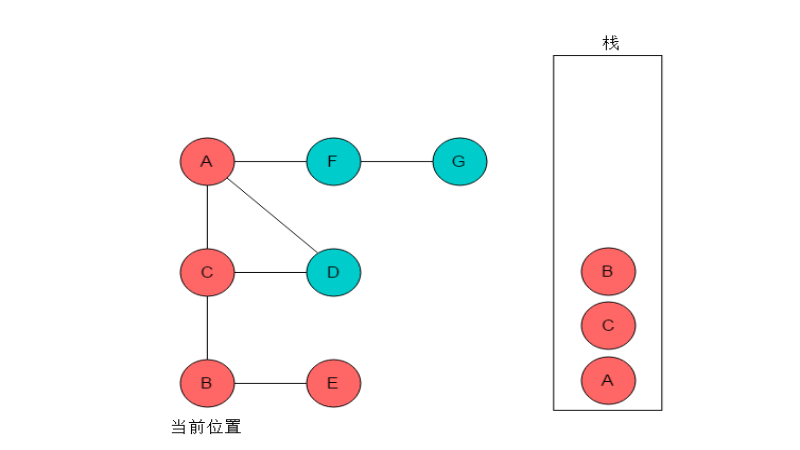
深度优先遍历顾名思义,以“深”作为优先条件,也就是不顾一切的向前走,走到哪算哪。就像一个愣头青想也不想,也不规划就是往前走,只要是没有走过的地方我就往前走,那要是到了某个地方能通到的地方都走过了或者走进了死胡同没路走了怎么办?那就原路返回,看看刚才走过的地方有没有通往没走过的地方的路。很好理解吧!
深度优先遍历的策略就是从一个顶点出发访问下一个未被访问的临接顶点,再从该顶点继续访问下一个未被访问的临接顶点。若当前顶点相连的节点均被访问过,则返回上一顶点作为当前节点重复上述操作,依次递归,直到所有节点均被访问过。

以上图为例,以A作为起点,先到达B(也可以先到F或C,无所谓),然后到F,再到H,再到G。此时可通往B、C、E,发现B已被访问过了,于是在C、E中选择一个。以C为例,然后到D,发现没路了。此时所有节点未被全部访问,则往回走到C,发现C通往的节点都被访问过了。再往回走到G,G到E,此时所有节点都被访问过,遍历结束。所以遍历顺序应该是A->B->F->H->G->C->D,G->E。
接下来我们来谈实现逻辑,这里有几个问题
- 当节点走进死胡同时如何回溯找上一结点?这就意味着必须有一个数据结构来存储节点的访问顺序,且可按从后加入的节点向早加入的节点顺序访问,这与栈后进先出的思想完全吻合,因此可设置一个栈对象来存储节点访问顺序。每访问一个节点就将其入栈,走进死胡同时栈顶元素出栈,访问接下来的栈顶元素。
- 如何判断节点是否访问过?很简单,设置一个boolean类型的数组,大小与节点数量相同,初始值均为false,表示均未被访问,每访问一个节点,就将布尔数组对应的位置设为true表示已访问。需要判断是否已被访问过时只需要判断是否为true即可。
- 遍历的终止条件是什么?在我早期看的一本参考书里将终止条件设置为栈空时结束遍历。但其实这样很不科学,想想我们上面那个案例,当E被访问后,其实此时遍历就已经完成了,但栈并不为空,程序还会继续回溯,直到把所有顶点全部回溯一遍。这种方式当然在不知道顶点数量时还是可行的,但是存在大量的冗余操作,在本文的程序中我们是知道节点数量的,因此只需判断已被访问的节点数量是否与总节点数量相等即可。
在写核心程序之前,我们还需要一个辅助函数,即获取与当前节点直接相连的下一个节点序号,邻接表与邻接矩阵实现遍历的不同点也就在这个辅助函数。
//返回顶点vi在vj后的后继邻接顶点序号,若j=-1,则返回vi的第一个邻接顶点序号;
//若不存在后继邻接顶点,则返回-1
@Override
protected int next(int i, int j) {
if(i >= 0 && j >= -1 && i != j && i < this.vertexCount() && j < this.vertexCount()) {
//查找指定节点
if(j == -1) return rowlist[i].column;
boolean flag = false;
Triple node = rowlist[i];
while(node != null){
if(node.column == j) {
flag = true;
break;
}
node = node.next;
}
//并未找到指定节点,直接返回-1
if(!flag) return -1;
//当前节点的下一个节点不为空,返回下一个节点的列号
if(node.next != null) return node.next.column;
}
return -1;
}输入的两个参数一个是当前节点序号,另一个是当前相连节点序号,获取的是下一个相连节点序号。若j=-1则返回相连的第一个节点序号,若无下一个相连节点,则返回-1。
首先判断输入是否合法,不合法直接返回-1。然后判断j是否为-1,若是则直接返回邻接表矩阵对应位置的结点(即第一个相连节点)的列号。然后循环遍历链表查找当前j对应的节点,并设置一个标志位flag表示是否成功找到,查找完毕后判断flag是否为false,若是,则表示根本无这个节点,返回-1,否则判断是否还有下一个节点(是否是链表尾),若有则返回下一节点的列号,否则返回-1。
万事俱备,下面开始讲深度优先遍历的核心代码,话不多说,直接上代码,为了不让读者混乱,我采用了非递归的方式实现。
//深度优先遍历,从顶点vi开始
@Override
public void DFSTraverse(int i) {
if(i < 0 || i >= vertexCount())
return;
var stack = new Stack<Integer>(); //节点序号存储栈
boolean[] visited = new boolean[vertexCount()]; //元素是否被访问过标志数组
int num = 0; //已被访问节点数量
visited[i] = true;
stack.push(i);
num++;
while(num != vertexCount()){
int nextNodeIndex = depthfs(i, visited); //找到当前节点的第一个连通节点
if(nextNodeIndex != -1){ //找到了当前节点的一个连通节点
visited[nextNodeIndex] = true;
stack.push(nextNodeIndex);
num++;
System.out.print(vertexlist.get(i) + "->" + vertexlist.get(nextNodeIndex) + " ");
i = nextNodeIndex;
}else{ //未找到当前节点的连通节点
stack.pop(); //出栈
if(stack.empty()) return; //出栈后栈为空,表示已无任何节点与剩下的节点连通
i = stack.peek();
}
}
}
//从顶点vi出发进行深度优先搜索,找到一个未被访问的连通顶点,未找到则返回-1
private int depthfs(int i, boolean visited[]){
int nextNodeIndex = next(i, -1); //找到当前节点的第一个连通节点
if(nextNodeIndex == -1) return -1; //当前节点没有连通节点,直接返回-1
while(visited[nextNodeIndex]){ //遍历寻找下一个未被访问的连通顶点
nextNodeIndex = next(i, nextNodeIndex);
if(nextNodeIndex == -1)
break;
}
if(nextNodeIndex == -1) return -1; //所有连通顶点都被访问过,返回-1
return nextNodeIndex;
}我们一点一点来剖析。首先判断输入的起始顶点是否合法,若不合法直接结束(当然抛出错误也是可以的)。紧接着初始化我上面讲到的三个变量,节点访问顺序栈、访问布尔数组以及已被访问的节点数量。接下来一个核心while循环,终止条件为已被访问的节点数量和节点总数相等。循环体内首先调用depthfs寻找当前节点的下一个直连节点。下面我们来看一下depthfs函数。
首先因为是首次访问,先获取其第一个相连节点(j设置为-1即可),判断是否为-1,为-1表示根本没有相连节点,该节点无法通往任何其他节点,则此时有两种情况,其逻辑在上面的while循环里,待会说,此处直接返回-1。接下来的代码表示存在第一个相连节点,那么循环查找第一个未被访问过的相连节点,如果找到的结点序号为-1,表示已经全部找完了也没找到,则跳出循环并返回-1,再往下则表示找到了,返回该节点序号。
回到核心while循环,调用depthfs函数后,判断返回的是不是-1,如果不是-1表示找到了下一个节点,这个节点就是接下来要访问的。于是将其访问数组对应位设为true,入栈,被访问节点数量+1,当前节点设置为该节点。如果返回的是-1,表示压根没找着,走进了死胡同,那么此时存在两种情况
- 已经访问完全部节点,程序结束
- 未访问完全部节点,回溯
于是,先进行出栈操作,然后判断是否栈空,栈空表示没节点了,已经全部访问完了,直接结束程序。否则获取栈顶元素作为当前节点,到下一轮循环时,如果此时已经访问完了全部节点则循环结束,否则以栈顶元素(上一节点)作为当前节点继续遍历。
最终输出结果为:
三、广度优先遍历
广度优先遍历的重点在于“广”,每次走的时候都将当前所有能到的地方全部走一遍,不留后遗症,避免后面路走不通了再回头看走过的地方有没有路到没去过的地方,显然这是一个有点头脑的人。
广度优先遍历的策略就是从一个顶点出发遍历所有直达节点,再对每一个直达节点重复上述操作,其实和树的层次遍历一模一样。下面依然给出一个案例讲解。
依然是这张图,现在以广度优先遍历的策略来遍历。从A出发,依次遍历C、B、F。然后从C出发到达D,再从B出发,直连的F已经访问过了不考虑。再从F出发到达H。再从D出发没有直连节点,再从H出发到达G。再从G出发,直连的B、C已经访问过,到达E。再从E出发,没有直达的节点,遍历结束。
这么说似乎有些模糊,和层次遍历一样,广度优先遍历也是借助队列实现的。我再从队列的角度讲一遍就明白了。
从A出发,A入队,此时队列为A
- A出队,访问A,C、B、F入队,此时队列为C、B、F
- C出队,访问C,D入队,此时队列为B、F、D
- B出队,访问B,此时队列为F、D
- F出队,访问F,H入队,此时队列为D、H
- D出队,访问D,此时队列为H
- H出队,访问H,G入队,此时队列为G
- G出队,访问G,E入队,此时队列为E
- E出队,访问E,此时队列为空,遍历结束
由上,在实现广度优先遍历时:
- 需要一个队列,存储节点访问逻辑顺序
- 终止条件为访问后队列为空
- 访问逻辑为先队头出队,访问该出队队头,将队头直连的未访问节点插入队尾
话不多说,上代码
//图的广度优先遍历,从顶点vi出发
@Override
public void BFSTraverse(int i) {
if(i < 0 || i >= vertexCount())
return;
var queue = new LinkedList<Integer>(); //节点序号存储队列
boolean[] visited = new boolean[vertexCount()]; //元素是否被访问过标志数组
visited[i] = true; //访问当前节点
queue.offer(i); //当前节点入队
while(true){
i = queue.peek();
queue.poll(); //出队队头
breadthfs(i, visited, queue); //所有与当前节点相连的未访问节点入队
if(queue.isEmpty()) break;
}
}
//从vi出发进行广度优先搜索,找到全部相连节点,并加入队列
private void breadthfs(int i, boolean[] visited, LinkedList<Integer> queue){
Triple node = rowlist[i];
if(node == null) return; //没有与当前节点相连的节点
while(node != null){ //循环将链表中全部节点加入队列
if(!visited[node.column]) { //若该相连节点未被访问过,入队
System.out.print(vertexlist.get(i) + "->" + vertexlist.get(node.column) + " ");
queue.offer(node.column);
visited[node.column] = true;
}
node = node.next;
}
}首先判断出发顶点序号是否合法,若不合法直接停止遍历。紧接着初始化队列和访问数组,这里的队列使用的是JDK中的LinkedList,该数据结构既可用作顺序链表,也可用作顺序队列。然后将出发点入队,并标记为已访问。下面是核心while循环,一直迭代直到满足队列为空,遍历结束。循环体中即对应上述的访问逻辑,先获取队头节点作为当前访问节点,然后队头节点出队,再通过breadthfs将所有与当前节点直连的节点入队。最后判断队列是否为空,为空则遍历结束。下面来看一下breadthfs函数。
首先获取邻接表数组对应节点,判断该节点是否存在,若不存在表示没有与当前节点相连的节点,直接返回即可。接下来就需要去遍历链表了,对每个链表节点,若其列号未被访问过,则直接入队,并标记为已访问。事实上,该链表上所有节点就是对应该位置相连的所有节点,因此逻辑成立。
最后的遍历结果如下:



帖子还没人回复快来抢沙发