转载声明:文章来源https://blog.csdn.net/weixin_63267854/article/details/127776476
线索二叉树
1 线索二叉树基本概念
如果想直接看构造线索二叉树的友友们,直接跳到第二部分
在谈线索二叉树前,我们先谈谈什么时线索二叉树
所谓线索二叉树就是将二叉链表中的空指针改为指向前趋和后继的线索。
对于n个结点的指针,就相应的有n+1的空指针域,线索二叉树就是将这些空指针域利用起来!
我们知道二叉树遍历次序有先序遍历,中序遍历,后序遍历,这三种遍历次序对应的输出结果分别对应先序序列,中序序列,后序序列。而线索二叉树中的前趋和后继就是指的序列中位置的前趋和后继!举例:对于如下二叉树

其中序输出序列为:CBEGDFA,所以对于E结点其前趋为B,后继为G。
理解的前趋后继,下面谈谈如何将二叉树修改成线索二叉树!
如果结点左指针为空,就将该指针指向结点在序列中的前驱。如果结点右指针为空,就将该指针指向结点在序列中的后继。
为了弄清指针指向的时左右子树还是前驱后继,我们在结点中增加两个标志域LTag和RLag

这种结点结构的构成的二叉树叫线索二叉树
对应的存储结构叫做线索链表
结点中指向前驱后继的指针叫做线索。
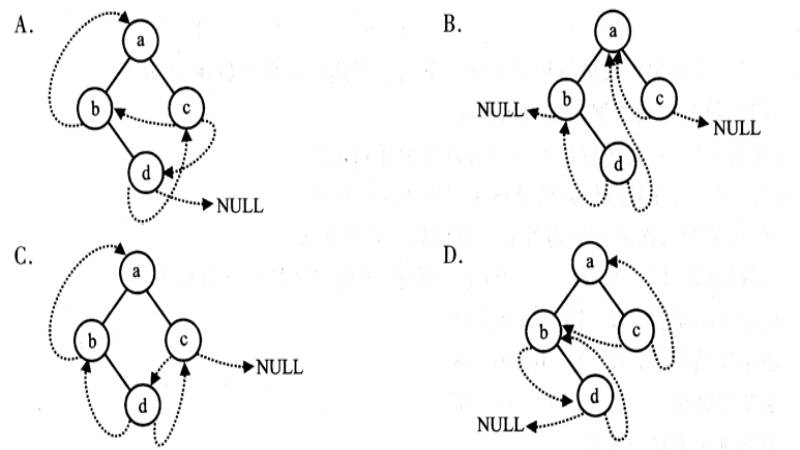
了解完线索二叉树的基本概念,来看个例子,看看其指针指向:如图(a)所示为中序线索二叉树,与其对应的中序线索链表如图(b)所示。
其中实线为指针(指向左、右子树),虚线为线索(指向前驱和后继)。

可以看出:线索二叉树仿照线性表的存储结构
在二叉树的线索链表上也添加一个头节点,并令其lchild域的指针指向二叉树的根节点,令其rchild域的指针指向中序遍历时访问的最后一个节点;
同时,令二叉树中序序列中第一个节点的lchild域指针和最后一个节点的rchild域指针均指向头节点。(中序序列第一个结点就是二叉树最左边的结点和最右边的结点)
这好比为二叉树建立了一个双向线索链表,既可从第一个节点起顺后继进行遍历,也可从最后一个节点起顺前驱进行遍历。
2 构造线索二叉树
构造线索二叉树的过程就是将二叉链表中的空指针改为指向前趋和后继的线索的过程。也就是说二叉树线索化就是修改空指针的过程。
由于前趋和后继只有在遍历的时候才能获得,所以按照不同的遍历次序对二叉树线索化,可以得到分别得到先序线索二叉树,中序线索二叉树,后续线索二叉树。
在讲解构造线索二叉树前,相信二叉树的遍历大家都很清楚了,访问结点的先后顺序时不变的(框架不变)。所谓先中后遍历二叉树就是将输出语句放在不同的位置,如下:
void prevOrder(BinaryTreeNode* root)
{
if (root == NULL)
{
cout << "NULL->";
return;
}
//cout << root->data << "->";//放在此处就是先序遍历
prevOrder(root->left);
//cout << root->data << "->";//放在此处就是中序遍历
prevOrder(root->right);
//cout << root->data << "->";//放在此处就是后序遍历
}这里先对构建线索二叉树进行总结,友友们没看懂没关系,可以向下看,看完三种线索二叉树的构建再回来读这部分一定会有不一样的收获!
将修改空指针的操作和记录前趋节点的操作放在放在二叉树遍历的不同位置,就衍生出先序线索二叉树,中序线索二叉树,后续线索二叉树。
为了记下遍历过程中访问结点的先后关系,便于当前节点的线索化,左指针指向前前趋,右指针指向后继。设置一个指针pre始终指向刚刚访问过的结点,而p指针指向当前结点
这里友友们就右疑问了?当前结点要改变左指针,也要改变右指针。不应该设置三个指针,prev指向前趋,next指向后继,p指向当前节点嘛?答案是不用的。我们每次修改空指针,都改变当前节点的左指针,改变前趋(也就是prev)的右指针。这样再遍历过后除了,除了序列的最后一个节点的后继没有修改外,其余节点均被完全线索化了。来看看个图就明白了:

记住:当前节点的左指针,改变前趋(也就是prev)的右指针
对于当前节点C而言,修改左指针,遍历一次后C成为前趋,修改前趋的右指针(C的后继),这样C的左右指针都做了修改!
2.1 中序线索二叉树的构建
在修改空指针前我们需要记下当前结点的前驱后继!所以设置一个指针prev始终指向刚刚访问过的结点,而p指针指向当前结点,在构造中序线索二叉树前,我们先理解pre指针和p指针时如何记录当前结点和前趋的,这样能更有利于我们理解中序二叉树的构建:
//将以p为根的二叉树线索化的部分代码
void InThreading(BTNode* p,BTNode*& prev) {
//if (!root)return;//可以写但很多余
//prev是全局定义好的变量,用于指向刚刚访问过的结点
if (p) {
InThreading(p->left,prev);
prev = p;
InThreading(p->right,prev);
}
}可以看到,和遍历输出二叉链表的代码实现很像!p非空?那就递归左子树线索化,记录根结点prev = p;,再右子树线索化!
prev的初始值指向线索二叉树的头节点Thrt,对于中序第一个结点,它的前趋就是二叉搜索树的头节点
上面代码,每一层递归都记录下的当前结点和上一个结点:每一层递归中当前结点为p,当前结点的前趋为prev。下一步接着加入修改空指针的操作:
//将以p为根的二叉树线索化
void InThreading(BTNode* p, BTNode*& prev) {
//if (!root)return;//可以写但很多余
//prev是全局定义好的变量,用于指向刚刚访问过的结点
if (p) {
InThreading(p->left, prev);
if (!p->left) {
p->LTag = 1;//标记p->left为左线索
p->left = prev;//指向前趋
}
else p->LTag = 0;//标记p->left指向左子树
if (!prev->right) {
prev->RTag = 1;//标记p->right为右线索
prev->right = p;//指向后继
}
else prev->RTag = 0;//标记p->right指向右子树
prev = p;
InThreading(p->right, prev);
}
}上面说过,我们每次修改空指针,都改变当前节点的左指针,改变前趋(也就是prev)的右指针。这样再遍历过后除了,除了序列的最后一个节点的后继没有修改外,其余节点均被完全线索化了。所以真正的代码实现我们还需要对序列最后一个节点的后继线索化!,下面是完整的线索化二叉树实现:
//将以p为根的二叉树线索化
void InThreading(BTNode* p, BTNode*& prev) {
//if (!root)return;//可以写但很多余
//prev是全局定义好的变量,用于指向刚刚访问过的结点
if (p) {
InThreading(p->left, prev);
if (!p->left) {
p->LTag = 1;//标记p->left为左线索
p->left = prev;//指向前趋
}
else p->LTag = 0;//标记p->left指向左子树
if (!prev->right) {
prev->RTag = 1;//标记p->right为右线索
prev->right = p;//指向后继
}
else prev->RTag = 0;//标记p->right指向右子树
prev = p;
InThreading(p->right, prev);
}
}
//中序遍历二叉树T,并将线索化,Thrt指向头节点(线索二叉树的头节点)
void InOrderThreading(BTNode*& Thrt, BTNode* root) {
Thrt = new BTNode;//建立头节点
Thrt->LTag = 0;//头节点有左孩子,若树非空,左孩子为树根。若树空,左孩子指向其自己。
Thrt->RTag = 1;//头节点右孩子指向序列最后一个节点
Thrt->right = Thrt;//右孩子初始化指向自己
if (!root)Thrt->left = Thrt;
else {
Thrt->left = root;
BTNode* prev = Thrt;//前趋节点,初始化指向头节点
InThreading(root, prev);
prev->right = Thrt;//递归出来prev指向序列最后一个节点,对最后一个节点序列化
prev->RTag = 1;
Thrt->right = prev;
}
}理解完了中序遍历,相信大家也能大概懂得了先序后续线索二叉树的方法咯,就是改变记录前趋的位置,修改空指针的位置
2.2 先序线索二叉树的构建
还是一样,在修改空指针前我们需要记下当前结点的前驱后继!所以设置一个指针prev始终指向刚刚访问过的结点,而p指针指向当前结点,在构造先序线索二叉树前,我们先理解pre指针和p指针时如何记录当前结点和前趋的,这样能更有利于我们理解先二叉树的构建:
//将以p为根的二叉树线索化
void InThreading(BTNode* p, BTNode*& prev) {
//if (!root)return;//可以写但很多余
//prev是全局定义好的变量,用于指向刚刚访问过的结点
if (p) {
prev = p;
InThreading(pleft, prev);
InThreading(p->right, prev);
}
}可以发现和中序相比就是将prev=p移动的了位置
下面就是修改空指针了,此处有点小修改,因为先序线索二叉树可能需要再访问左右子树前,修改左右指针,这直接影响我们原本遍历二叉树所以我们,先将左指针存储起来,再修改左指针:
//将以p为根的二叉树线索化
void InThreading(BTNode* p, BTNode*& prev) {
//if (!root)return;//可以写但很多余
//prev是全局定义好的变量,用于指向刚刚访问过的结点
if (p) {
BTNode* pleft = p->left;//先存储左指针,防止下面修改左指针映像二叉树遍历!
if (!p->left) {
p->LTag = 1;//标记p->left为左线索
p->left = prev;//指向前趋
}
else p->LTag = 0;//标记p->left指向左子树
if (!prev->right) {
prev->RTag = 1;//标记p->right为右线索
prev->right = p;//指向后继
}
else prev->RTag = 0;//标记p->right指向右子树
prev = p;
InThreading(pleft, prev);
InThreading(p->right, prev);
}
}和中序一样需要对序列最后一个节点序列化,完整实现如下:
//将以p为根的二叉树线索化
void InThreading(BTNode* p, BTNode*& prev) {
//if (!root)return;//可以写但很多余
//prev是全局定义好的变量,用于指向刚刚访问过的结点
if (p) {
BTNode* pleft = p->left;//用于临时存储当前节点的left,以放NULL修改后死循环!
if (!p->left) {
p->LTag = 1;//标记p->left为左线索
p->left = prev;//指向前趋
}
else p->LTag = 0;//标记p->left指向左子树
if (!prev->right) {
prev->RTag = 1;//标记p->right为右线索
prev->right = p;//指向后继
}
else prev->RTag = 0;//标记p->right指向右子树
prev = p;
InThreading(pleft, prev);
InThreading(p->right, prev);
}
}
//中序遍历二叉树T,并将线索化,Thrt指向头节点(线索二叉树的头节点)
void InOrderThreading(BTNode*& Thrt, BTNode* root) {
Thrt = new BTNode;//建立头节点
Thrt->LTag = 0;//头节点有左孩子,若树非空,左孩子为树根。若树空,左孩子指向其自己。
Thrt->RTag = 1;//头节点右孩子指向序列最后一个节点
Thrt->right = Thrt;//右孩子初始化指向自己
if (!root)Thrt->left = Thrt;
else {
Thrt->left = root;
BTNode* prev = Thrt;//前趋节点,初始化指向头节点
InThreading(root, prev);
prev->right = Thrt;//递归出来prev指向序列最后一个节点,对最后一个节点序列化
prev->RTag = 1;
Thrt->right = prev;
}
}2.3 后续线索二叉树的构建
经过上面两个讲解,大家坑定也知道了,后续线索二叉树就是将修改空指针和记录位置下移,但不同的是后续序列最后一个节点是不一定要序列化的因此还要判断,再序列化,代码实现:
//将以p为根的二叉树线索化
void InThreading(BTNode* p, BTNode*& prev) {
//if (!root)return;//可以写但很多余
//prev是全局定义好的变量,用于指向刚刚访问过的结点
if (p) {
InThreading(p->left, prev);
InThreading(p->right, prev);
if (!p->left) {
p->LTag = 1;//标记p->left为左线索
p->left = prev;//指向前趋
}
else p->LTag = 0;//标记p->left指向左子树
if (!prev->right) {
prev->RTag = 1;//标记p->right为右线索
prev->right = p;//指向后继
}
else prev->RTag = 0;//标记p->right指向右子树
prev = p;
}
}
//中序遍历二叉树T,并将线索化,Thrt指向头节点(线索二叉树的头节点)
void InOrderThreading(BTNode*& Thrt, BTNode* root) {
Thrt = new BTNode;//建立头节点
Thrt->LTag = 0;//头节点有左孩子,若树非空,左孩子为树根。若树空,左孩子指向其自己。
Thrt->RTag = 1;//头节点右孩子指向序列最后一个节点
Thrt->right = Thrt;//右孩子初始化指向自己
if (!root)Thrt->left = Thrt;
else {
Thrt->left = root;
BTNode* prev = Thrt;//前趋节点,初始化指向头节点
InThreading(root, prev);
if (!prev->right) {
prev->right = Thrt;//递归出来prev指向序列最后一个节点,对最后一个节点序列化
prev->RTag = 1;
}
else {
prev->RTag = 0;
}
Thrt->right = prev;
}
}3 遍历线索二叉树
3.1 找指定节点的前驱后继
由于有了节点的前驱和后继信息,线索二叉树的遍历和在指定次序下查找节点的前驱和后继算法都变得简单了。因此,若需经常查找节点在所遍历线性序列中的前驱和后继,则采用线索链表作为存储结构。
下面分3种情况讨论在线索二叉树中如何查找节点的前驱和后继。
在中序线索二叉树中查找
查找p指针所指节点的前驱:
若p- > LTag为1,则p的左链指示其前驱;
若p->LTag为0,则说明p有左子树,节点的前驱是遍历左子树时最后访问的一个节点(左子树中最右下的节点)。
查找p指针所指节点的后继:
若p->RTag为1,则p的右链指示其后继
若p->RTag为0,则说明p有右子树。根据中序遍历的规律可知,节点的后继应是遍历其右子树时访问的第一个节点,即右子树中最左下的节点。
在先序线索二叉树中查找
查找p指针所指节点的前驱:
若p- > LTag为1,则p的左链指示其前驱;
若p- > LTag为0,则说明p有左子树。此时p的前驱有两种情况:若*p是其双亲的左孩则其前驱为其双亲节点;否则应是其双亲的左子树上先序遍历最后访问到的节点。
查找p指针所指节点的后继:
若p- >RTag为1,则p的右链指示其后继;
若p- >RTag为0,则说明p有右子树。按先序遍历的规则可知,*p的后继必为其左子树根(若存在)或右子树根。
在后序线索二叉树中查找
查找p指针所指节点的前驱:
若p->LTag为1,则p的左链指示其前驱;
若p->LTag为0,当p- > RTag也为0时,则p的右链指示其前驱;若p- >LTag为0,而p->RTag为1时,则p的左链指示其前驱。
查找p指针所指节点的后继情况比较复杂,分以下情况讨论:
若*p是二叉树的根,则其后继为空;
若*p是其双亲的右孩子,则其后继为双亲节点;
若*p是其双亲的左孩子,且*p没有右兄弟,则其后继为双亲节点;
若*p是其双亲的左孩子,且*p有右兄弟,则其后继为双亲的右子树上按后序遍历列出的第一个节点(右子树中最左下的叶节点)。
3.2 遍历二叉树
你当然可以直接递归遍历,根据标记判断当前节点是否有左右子树。但我们知道递归遍历二叉树时间复杂度和空间复杂度都是O(N)。但这样丝毫没有发挥线索二叉树的优势,线索二叉树的非递归遍历才是一大亮点!
这里以中序线索二叉树为例,在理解中序线索二叉树非递归遍历前,先要清楚线索二叉树是如何非递归遍历的算法思路:
指针p指向根节点。(也可以是子树的根)
p为非空树或遍历未结束时,循环执行以下操作:
沿左孩子向下,到达最左下节点*p,它是该子树中序遍历的第一个节点;访问*p;
沿右线索反复查找当前节点*p的后继节点并访问后继节点,直至右
线索为0或者遍历结束;
转向p的右子树。
下面是完整的线索二叉树,非递归遍历顺序,为了便于理解,这里简述其中过程,
开始p指针指向A
然后循环找到当前子树最左下角的节点M,并输出!
M通过右索引访问输出N(此时循环结束,N没有右索引)
循环结束就将指针指向该节点的右孩子(也就是新的根节点了)
下图红线是中序线索二叉树遍历输出过程,每一个红线下方的节点都是当前子树的最左下节点。把握住子树的最左下节是中序遍历的头,右线索是直接后继。

下面是代码实现:
void InOrderTraverse(BTNode* T)
{
BTNode* p = T->left;//线索二叉树头节点的左指针指向实际二叉树的头
while (p != T)
{
//1. 循环找到当前子树的左下角,开始以四字节单元访问!
while (p->LTag == 0)
p = p->left;
cout << p->data;
//2. 通过右索引访问直接后继
while (p->RTag == 1 && p->right != T)
{
p = p->right;
cout << p->data;
}
//3. 四字节单元访问完,指向右孩子,寻找下一个四字节!
p = p->right;
}
}


帖子还没人回复快来抢沙发