转载声明:文章来源https://blog.csdn.net/yandadzf/article/details/141400211
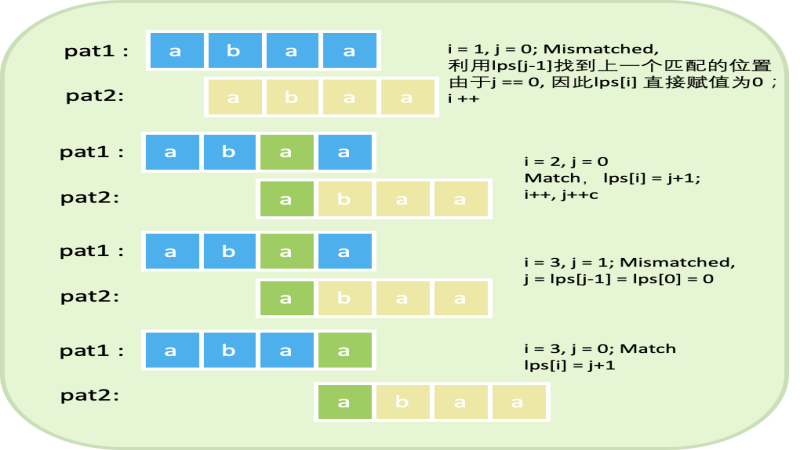
一、了解模式匹配算法(KMP算法)
字符串的模式匹配是计算机科学中的一个基本问题,它旨在找出一个文本字符串(text)中是否包含一个模式字符串(pattern),以及该模式字符串在文本字符串中的位置。有多种算法可以解决这一问题,其中Knuth-Morris-Pratt(KMP)算法因其高效性而广受欢迎。
1、简单的模式匹配算法(朴素模式匹配算法)
朴素模式匹配算法是最直观的方法,它遍历文本字符串的每一个字符作为起点,然后尝试将模式字符串与文本字符串的相应子串进行匹配。如果匹配成功,则返回模式字符串在文本中的位置;如果遍历完所有可能的起点后仍未找到匹配,则返回未找到。这种方法的时间复杂度在最坏情况下为O(n*m),其中n是文本字符串的长度,m是模式字符串的长度。
缺点:当模式字符串中存在大量重复前缀且未匹配到模式字符串的末尾时,会重复检查文本中的相同字符。
2、KMP算法
KMP算法通过预处理模式字符串来避免上述重复检查的问题,从而提高效率。算法的核心在于构建一个部分匹配表(也称为“前缀函数”或“失败函数”),用于指导在不匹配时如何移动模式字符串。
部分匹配表(Prefix Function):对于模式字符串P的每个位置i(从1开始),计算最长的相同前缀和后缀的长度(不包括整个字符串本身)。例如,对于模式"ABABD",其部分匹配表为[0, 0, 0, 1, 2]。
算法流程:
预处理模式字符串,构建部分匹配表。
遍历文本字符串,使用两个指针分别指向文本和模式的当前位置。
如果当前字符匹配,则两个指针都向前移动。
如果不匹配,则将模式字符串的指针回退到部分匹配表中指定的位置,文本字符串的指针不变,然后继续比较。
如果模式字符串的指针回退到0但仍不匹配,则文本字符串的指针向前移动一位,模式字符串的指针回到起始位置。
重复步骤3-5,直到找到匹配或遍历完文本字符串。
时间复杂度:KMP算法的时间复杂度为O(n+m),其中n是文本字符串的长度,m是模式字符串的长度。这是因为每个字符在文本和模式中最多被比较两次(一次在正常匹配过程中,一次在模式字符串内部根据部分匹配表回退时)。
二、简单的模式匹配算法
当我们想要在一个较长的字符串(称为主串或文本串)中找到一个较短的字符串(称为模式串或子串)的位置时,就可以使用这种简单模式匹配算法。比如,我们想在"hello world"这个字符串中找到"world"的位置。
简单模式匹配算法的基本思想是:将模式串与主串的每一个可能的起始位置进行匹配,直到找到完全匹配的子串或者搜索完所有的可能位置。
实现方法:
检查模式串长度:首先,算法会检查模式串的长度是否大于主串的长度。如果是,那么显然不可能在主串中找到模式串,因此直接返回某种表示未找到的值(但在这个实现中,它错误地返回了0,通常我们应该返回-1)。
初始化索引:接着,算法会初始化两个索引,i用于遍历主串,j用于遍历模式串。它们都从0开始。
遍历主串:然后,算法会进入一个循环,该循环会一直进行,直到i超出了模式串可能出现在主串中的最后一个起始位置(即i <= S->length - T->length)。这是因为,如果i已经比S->length - T->length还要大,那么从i开始就没有足够的空间来放下整个模式串了。
匹配过程:在循环内部,算法会逐个字符地比较模式串和主串从当前i位置开始的子串。如果所有字符都匹配(即j达到了模式串的长度T->length),那么算法就找到了一个匹配,并返回基于1的索引(即i + 1,因为索引通常从0开始,但返回时可能希望从1开始计数以便更直观地表示位置)。
不匹配处理:如果在匹配过程中发现不匹配的字符,算法会重置模式串的索引j为0(从头开始匹配模式串),并将主串的索引i增加1(尝试从主串的下一个位置开始匹配)。
返回未找到的值:如果循环结束后仍未找到匹配,算法会返回某种表示未找到的值(在这个实现中仍然是0,但更常见的是返回-1)。
// 简单模式匹配算法
int simpleStringSearch(SString* S, SString* T) {
if (T->length > S->length) return 0; // 检查模式串是否大于主串
int i = 0; // 主串索引
int j = 0; // 模式串索引
while (i <= S->length - T->length) { // 迭代主串
if (S->ch[i + j] == T->ch[j]) {
j++;
if (j == T->length) return i + 1; // 找到匹配,返回基于 1 的索引
}
else {
i++; // 主串索引增加
j = 0; // 重置模式串索引
}
}
return 0; // 找不到匹配,返回 0
}时间复杂度分析
最坏情况:
在最坏的情况下,主串 S 和模式串 T 的字符几乎完全相同,但只有最后一个字符不匹配。例如,主串为 "aaaaaa",模式串为 "aaaaab"。
在这种情况下,算法会遍历主串的每一个字符,并在每次比较时重置模式串索引 j,导致主串的每个字符都被比较多次。
时间复杂度为 O(n⋅m),其中 n 是主串的长度,m 是模式串的长度。
最好情况:
在最好情况下,主串的第一个字符就与模式串的第一个字符匹配,且模式串的所有字符都能在主串的开头找到。
在这种情况下,算法只需进行一次比较,时间复杂度为 O(n)。
平均情况:
平均情况下,算法的性能取决于主串和模式串的字符分布。一般情况下,假设字符是随机分布的,时间复杂度大约为O(n+m),因为每个字符大约会被比较一次。
空间复杂度分析
该算法只使用了常量级的额外空间来存储变量 i 和 j,没有使用额外的数据结构来存储中间结果。
因此,空间复杂度为 O(1)。
三、KMP算法
KMP算法的核心想法
KMP算法(Knuth-Morris-Pratt算法)是一种高效的字符串匹配算法。它的核心想法是,在模式串与主串的匹配过程中,当遇到不匹配的情况时,能够利用之前已经匹配过的信息,避免从头开始重新匹配模式串,从而提高匹配效率。
为了实现这一点,KMP算法会预处理模式串,生成一个next数组(也称为部分匹配表或失败函数)。这个数组记录了模式串中每个位置之前的最长相等前后缀的长度(实际上,这个长度会加1作为数组索引,且数组的第一个元素通常不使用或设置为-1,用于特殊处理)。
KMP算法的实现步骤和方法
预处理模式串:
生成next数组。遍历模式串,对于每个位置,计算该位置之前的最长相等前后缀的长度(注意是长度加1作为数组索引),并将结果存储在next数组中。特别地,如果某个位置没有这样的前后缀,next值可能设置为0或-1(取决于具体实现)。
匹配过程:
初始化两个指针i和j,分别指向主串和模式串的起始位置。
遍历主串,直到i达到主串的末尾或找到一个完整的模式串匹配。
在每次迭代中,比较S->ch[i](主串当前字符)和T->ch[j](模式串当前字符):
如果字符相等,则同时移动i和j到下一个位置。
如果字符不相等,则根据next[j]的值移动j。这里next[j]给出了在不匹配时模式串应该跳到的下一个位置(基于之前计算的最长相等前后缀信息)。
如果next[j]的值小于0(这通常表示模式串的第一个字符就不匹配,或者next数组的特殊处理),则将j重置为0(从头开始匹配模式串),但此时i也应该增加1(因为主串的当前位置已经与模式串的第一个字符不匹配过了)。
如果在某个位置j达到了模式串的末尾,则说明找到了一个匹配,返回该匹配在主串中的起始位置(注意,这里返回的是基于1的索引,而您的函数中使用了i - j + 1来计算这个值,这是正确的,因为i是主串的当前位置,j是模式串的末尾位置,它们之间的差值加上1就是匹配的起始位置)。
返回结果:
如果遍历完主串都没有找到匹配,则返回0或某个特定的值来表示未找到匹配。
代码实现:
// KMP算法
// i 一直前进
int kmpSearch(SString* S, SString* T, int next[]) {
if (T->length > S->length) return 0; // 检查模式串是否大于主串
int i = 0; // 主串索引
int j = 0; // 模式串索引
while (i < S->length) { // 迭代主串
if (S->ch[i] == T->ch[j]) {
j++; // 匹配成功,模式串索引增加
i++; // 主串索引增加
if (j >= T->length) return i - j + 1; // 找到匹配,返回匹配位置
}
else {
j = next[j]; // 失败时,根据 next 数组更新模式串索引
if (j < 0) { // 如果 j < 0,说明模式串已经没有可回退的部分
i++; // 主串索引增加
j = 0; // 重置模式串索引
}
}
}
return 0; // 找不到匹配,返回 0
}时间复杂度
预处理阶段:
在 KMP 算法中,首先需要构建 next 数组,这个过程的时间复杂度是 O(m),其中 m 是模式串 T 的长度。
next 数组的构建是通过遍历模式串来完成的,时间复杂度为 O(m)。
匹配阶段:
在匹配主串 S 和模式串 T 的过程中,两个指针 i 和 j 分别遍历主串和模式串。
在最坏的情况下,当主串和模式串不匹配时,指针 i 可能会遍历整个主串,而 j 也会根据 next 数组进行回退。
由于每个字符至多被访问两次(一次是匹配时,另一次是失败时),因此匹配阶段的时间复杂度为 O(n),其中 n 是主串 S 的长度。
总时间复杂度:
综合考虑预处理和匹配阶段,KMP 算法的总时间复杂度为:O(m+n)
其中 m 是模式串的长度,n 是主串的长度。
空间复杂度
额外空间:
KMP 算法使用了一个 next 数组来存储模式串的部分匹配信息,next 数组的大小为 mm。
因此,KMP 算法的空间复杂度为 O(m)。
各种情况分析
最好情况:
在最好情况下,模式串的第一个字符就与主串的第一个字符匹配,且模式串中的所有字符都与主串匹配。这种情况下,时间复杂度为 O(n)(只需遍历主串一次),空间复杂度为 O(m)。
最坏情况:
最坏情况下,主串和模式串的字符几乎全部不匹配,导致每次都需要回退到 next 数组的开始位置。例如,主串为 "aaaaaa" 而模式串为 "aaab"。在这种情况下,时间复杂度仍然是 O(n),但常数因子可能较大;空间复杂度依然是 O(m)。
平均情况:
在平均情况下,KMP 算法的时间复杂度依然是 O(n),因为虽然有回退,但总体来看,字符的比较次数是线性的。空间复杂度仍然是 O(m)。
总结
KMP 算法的时间复杂度为 O(m+n),其中 m 是模式串的长度,n 是主串的长度。
KMP 算法的空间复杂度为 O(m)。
不论在最好、最坏还是平均情况下,KMP 算法的效率都优于简单的暴力匹配算法,特别是在处理长字符串时。
四、求next数组
核心思维
函数GetKmpNext的核心思维是计算并填充next的数组,该数组对于KMP(Knuth-Morris-Pratt)字符串匹配算法至关重要。next数组存储了模式串(即要搜索的字符串)中每个位置之前的最长相等前后缀的长度信息(实际上,存储的是长度加1的值,且数组的第一个元素通常设置为-1作为特殊情况处理)。这个信息允许KMP算法在发生不匹配时,不需要从模式串的开头重新匹配,而是根据next数组的值直接跳转到更合适的位置继续匹配,从而提高了匹配效率。
实现方式
变量定义
int j = 0;:用于遍历模式串S的当前位置。
next[0] = -1;:初始化next数组的第一个元素为-1,表示模式串的第一个字符之前没有任何字符(即没有前后缀)。
int k = -1;:作为辅助变量,用于在next数组中回溯。初始化为-1,与next[0]的值相对应,同时也用于处理模式串第一个字符的特殊情况。
循环计算next数组
使用while循环遍历模式串S的每一个字符(实际上是从第二个字符开始,因为第一个字符的next值已经初始化)。
在每次循环中,检查两个条件:
k == -1:表示当前没有可用的前后缀信息(即正在处理模式串的第一个字符,或者之前已经回溯到了模式串的开头)。
S->ch[j] == S->ch[k]:表示当前字符S[j]与通过next数组回溯到的位置k上的字符S[k]相等,找到了一个更长的相等前后缀。
如果任一条件为真,说明可以继续向前匹配,于是同时递增j和k,并将k的值(实际上是前后缀的长度加1)赋给next[j]。
如果两个条件都不为真,说明在当前位置发生了不匹配,此时需要根据next[k]的值回溯。即,将k更新为next[k],继续在模式串中向前查找是否有匹配的字符。
返回值
函数返回true,表示next数组计算成功。在这个实现中,没有考虑任何可能导致失败的情况(如S为空、S->length为0或next数组未正确分配空间),因此总是返回true。
示例说明
假设模式串S为"ABCABD",则GetKmpNext函数计算得到的next数组可能如下:
next[0] = -1(没有前后缀)
next[1] = 0('A'没有非空前后缀)
next[2] = 0('B'没有非空前后缀)
next[3] = 0('C'没有非空前后缀)
next[4] = 1('A'之前有一个字符'A'与之相等,即最长相等前后缀为"A")
next[5] = 2('B'之前有两个字符"AB"与之相等,但注意这里我们存储的是长度加1的值,即3,但通常实现中会减1以存储长度本身,不过这里我们按照函数的实现方式来说明)
注意:上面的next[5]的说明中关于长度加1的值有些混淆,实际上在大多数KMP算法的实现中,next[5]会存储的是长度2(即"AB"的长度),而不是3。但在这个函数的实现中,它实际上存储的是3(即长度加1),因为后续在KMP匹配算法中,我们会使用next[k] - 1来获取实际的长度。不过,为了保持解释的一致性,我们通常会说next数组存储的是“长度加1”的值,但在理解和应用时需要注意这一点。
代码实现:
// 求Next数组
bool GetKmpNext(const SString* S, int next[]) {
int j = 0; // 表示当前要求的 next[i]
next[0] = -1; // next[0] 初始化为 -1
int k = -1; // 记录上一个 next
while (j < S->length) {
if (k == -1 || S->ch[j] == S->ch[k]) {
j++;
k++;
next[j] = k; // 更新 next 数组
}
else {
k = next[k]; // 回退到上一个 next
}
}
return true; // 返回成功
}时间复杂度
循环结构:
函数中有一个 while 循环,条件是 j < S->length,这意味着循环的次数最多为模式串 S 的长度 m。
在每次迭代中,j 要么增加 1(当 S->ch[j] 和 S->ch[k] 匹配时),要么 k 被更新为 next[k](当不匹配时)。
因此,虽然 k 可能会多次更新,但每个字符最多只会被访问两次(一次通过 j,一次通过 k),所以总的访问次数是线性的。
总时间复杂度:
因此,GetKmpNext 函数的时间复杂度为:O(m)
其中 m 是模式串 S 的长度。
空间复杂度
额外空间:
函数使用了一个 next 数组来存储模式串的部分匹配信息,next 数组的大小为 m。
此外,函数中使用了几个整型变量 j、k,这些变量的空间消耗是常量级的。
总空间复杂度:
因此,GetKmpNext 函数的空间复杂度为:O(m)
主要的空间消耗来自于 next 数组。
总结
时间复杂度:O(m),其中 m 是模式串的长度。
空间复杂度:O(m),主要是由于 next 数组的存储需求。
五、使用示例
int main() {
SString S, T; // 主串和模式串
int next[MAXLEN]; // 存放next数组
// 初始化字符串
InitString(&S);
InitString(&T);
// 输入主串和模式串
StrCopy(&S, "ABABDABACDABABCABAB");
StrCopy(&T, "ABABCABAB");
// 获取next数组
GetKmpNext(&T, next);
// 使用KMP算法查找模式串
int position = kmpSearch(&S, &T, next);
// 输出结果
if (position > 0) {
printf("模式串 \"%s\" 在主串 \"%s\" 中首次出现的位置: %d\n", T.ch, S.ch, position);
} else {
printf("模式串 \"%s\" 在主串 \"%s\" 中未找到。\n", T.ch, S.ch);
}
return 0;
}
六、总代码
————————————————
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
原文链接:https://blog.csdn.net/yandadzf/article/details/141400211六、总代码
#include
#include
#define MAXLEN 255 // 定义字符串最大长度
typedef struct {
char ch[MAXLEN]; // 存储字符串的字符数组
int length; // 字符串的当前长度
} SString;
// 初始化字符串
void InitString(SString* S) {
if (S != NULL) { // 检查指针有效性
S->length = 0;
S->ch[S->length] = '\0'; // 确保字符串结束
}
}
// 赋值操作
void StrAssign(SString* dest, const SString* src) {
if (dest == NULL || src == NULL) return; // 检查指针有效性
// 复制长度
dest->length = src->length;
// 复制字符数组
for (int i = 0; i < src->length; i++) {
dest->ch[i] = src->ch[i];
}
// 添加结束符
dest->ch[dest->length] = '\0';
}
// 复制操作
bool StrCopy(SString* S, const char chars[]) {
if (S == NULL || chars == NULL) return false; // 检查指针是否有效
int i = 0;
S->length = 0;
while (chars[i] != '\0') {
if (S->length >= MAXLEN - 1) { // 最后一位用来标志结束
return false;
}
S->ch[S->length] = chars[i];
i++;
S->length++;
}
S->ch[S->length] = '\0'; // 确保字符串结束
return true;
}
// 打印字符串
void PrintString(const SString* S) {
if (S != NULL) {
printf("字符串内容: %s\n", S->ch);
printf("字符串长度: %d\n", S->length);
}
}
// 判空操作
bool StrEmpty(SString S) {
return S.length == 0; // 如果长度为0,则字符串为空
}
// 比较操作
int StrCompare(const SString* S, const SString* T) {
int lengthDiff = S->length - T->length; // 先比较长度
if (lengthDiff != 0) return lengthDiff; // 长度不同,返回差值
// 长度相同,逐个字符比较
for (int i = 0; i < S->length; i++) {
if (S->ch[i] > T->ch[i]) return 1; // S 大于 T
if (S->ch[i] < T->ch[i]) return -1; // S 小于 T
}
return 0; // 相等
}
// 求串长
int StrLength(SString* S) {
return S->length; // 返回字符串的长度
}
// 求子串
bool SubString(SString* Sub, SString* S, int pos, int len) {
if (pos < 1 || pos > S->length || len < 1) return false; // 检查位置和长度的有效性
if (pos + len - 1 > S->length) return false; // 检查是否超出原字符串范围
// 复制子串
for (int i = 0; i < len; i++) {
Sub->ch[i] = S->ch[pos - 1 + i]; // 逐个字符复制
}
Sub->length = len; // 设置子串长度
Sub->ch[Sub->length] = '\0';
return true; // 复制成功
}
// 串联接
bool Concat(SString* T, SString* S1, SString* S2) {
if (S1->length + S2->length >= MAXLEN) return false; // 检查是否超出最大长度
int i = 0;
// 复制第一个字符串
for (i = 0; i < S1->length; i++) {
T->ch[i] = S1->ch[i];
}
// 复制第二个字符串
for (i = 0; i < S2->length; i++) {
T->ch[S1->length + i] = S2->ch[i];
}
T->length = S1->length + S2->length; // 设置新字符串的长度
T->ch[T->length] = '\0';
return true; // 串联成功
}
// 8. 定位操作
// 函数功能:在字符串S中查找子串T,返回T在S中首次出现的位置。如果T不是S的子串,则返回0。
// 优化算法后续提供
int INdex(SString* S, SString* T) {
// 如果T的长度大于S的长度,则T不可能是S的子串,直接返回0。
if (T->length > S->length) return 0;
int cnt = 0; // 用于记录当前匹配的字符数量
// 外层循环,遍历S字符串,直到S中剩余的长度小于T的长度,此时无需继续比较。
for (int i = 0; i <= S->length - T->length; i++) {
cnt = 0; // 每次开始新的匹配时,重置计数器
// 内层循环,遍历T字符串,进行字符匹配
for (int j = 0; j < T->length; j++) {
// 如果S和T中的字符不匹配,则跳出内层循环
if (S->ch[i + j] != T->ch[j]) {
break;
}
cnt++; // 如果字符匹配,计数器加1
}
// 如果计数器值等于T的长度,说明T是S的子串,返回T在S中的起始位置(位置从1开始计数)
if (cnt == T->length) return i + 1;
}
// 如果遍历完S仍未找到T,则返回0
return 0;
}
// 9. 清空操作
void ClearString(SString* S) {
if (S != NULL) { // 检查指针有效性
S->length = 0;
S->ch[S->length] = '\0'; // 确保字符串结束
}
}
// 10. 销毁操作、
void DestroyString(SString* S) {
if (S != NULL) { // 检查指针有效性
S->length = 0;
S->ch[S->length] = '\0'; // 确保字符串结束
}
}
// 示例
void sy1() {
SString s1, s2, result, sub;
// 初始化字符串
InitString(&s1);
InitString(&s2);
InitString(&result);
InitString(&sub);
StrCopy(&s1, "Hello, World!");
// 复制操作
StrCopy(&s2, "Copy of Hello, World!");
// 打印字符串
PrintString(&s1);
PrintString(&s2);
// 判空操作
printf("s1 是否为空: %s\n", StrEmpty(s1) ? "是" : "否");
// 比较操作
int cmpResult = StrCompare(&s1, &s2);
printf("比较结果: %d\n", cmpResult);
// 求串长
printf("s1 的长度: %d\n", StrLength(&s1));
// 求子串
if (SubString(&sub, &s1, 8, 5)) { // 从第8个字符开始取5个字符
PrintString(&sub);
}
else {
printf("子串提取失败\n");
}
// 串联接
if (Concat(&result, &s1, &s2)) {
PrintString(&result);
}
else {
printf("串联失败\n");
}
SString WW;
char d[5] = "World";
for (int i = 0; i < 5; i++) WW.ch[i] = d[i];
WW.length = 5;
// 定位操作
int index = INdex(&result, &WW); // 查找 "World"
printf("\"World\" 在 s1 中的位置: %d\n", index);
// 清空操作
ClearString(&s1);
PrintString(&s1);
// 销毁操作(对于顺序存储,实际上只是清空)
// 注意:在顺序存储中,DestroyString 应该只是 ClearString
// 如果是动态分配的内存,则需要释放内存
//
}
// 简单模式匹配算法
int simpleStringSearch(SString* S, SString* T) {
if (T->length > S->length) return 0; // 检查模式串是否大于主串
int i = 0; // 主串索引
int j = 0; // 模式串索引
while (i <= S->length - T->length) { // 迭代主串
if (S->ch[i + j] == T->ch[j]) {
j++;
if (j == T->length) return i + 1; // 找到匹配,返回基于 1 的索引
}
else {
i++; // 主串索引增加
j = 0; // 重置模式串索引
}
}
return 0; // 找不到匹配,返回 0
}
// KMP算法
// i 一直前进
int kmpSearch(SString* S, SString* T, int next[]) {
if (T->length > S->length) return 0; // 检查模式串是否大于主串
int i = 0; // 主串索引
int j = 0; // 模式串索引
while (i < S->length) { // 迭代主串
if (S->ch[i] == T->ch[j]) {
j++; // 匹配成功,模式串索引增加
i++; // 主串索引增加
if (j >= T->length) return i - j + 1; // 找到匹配,返回匹配位置
}
else {
j = next[j]; // 失败时,根据 next 数组更新模式串索引
if (j < 0) { // 如果 j < 0,说明模式串已经没有可回退的部分
i++; // 主串索引增加
j = 0; // 重置模式串索引
}
}
}
return 0; // 找不到匹配,返回 0
}
// 求Next数组
bool GetKmpNext(const SString* S, int next[]) {
int j = 0; // 表示当前要求的 next[i]
next[0] = -1; // next[0] 初始化为 -1
int k = -1; // 记录上一个 next
while (j < S->length) {
if (k == -1 || S->ch[j] == S->ch[k]) {
j++;
k++;
next[j] = k; // 更新 next 数组
}
else {
k = next[k]; // 回退到上一个 next
}
}
return true; // 返回成功
}
int main() {
SString S, T; // 主串和模式串
int next[MAXLEN]; // 存放next数组
// 初始化字符串
InitString(&S);
InitString(&T);
// 输入主串和模式串
StrCopy(&S, "ABABDABACDABABCABAB");
StrCopy(&T, "ABABCABAB");
// 获取next数组
GetKmpNext(&T, next);
// 使用KMP算法查找模式串
int position = kmpSearch(&S, &T, next);
// 输出结果
if (position > 0) {
printf("模式串 \"%s\" 在主串 \"%s\" 中首次出现的位置: %d\n", T.ch, S.ch, position);
}
else {
printf("模式串 \"%s\" 在主串 \"%s\" 中未找到。\n", T.ch, S.ch);
}
return 0;
}七、总结
字符串模式匹配是计算机科学中的重要问题,尤其在文本处理、搜索引擎和数据分析等领域具有广泛应用。本文探讨了两种主要的模式匹配算法:朴素模式匹配算法和KMP算法。
朴素模式匹配算法:
实现简单,直接通过遍历主串的每个可能起始位置与模式串进行逐字符比较。
该算法在最坏情况下的时间复杂度为O(n⋅m),在处理长文本和复杂模式时效率较低。
由于缺乏优化,重复检查相同字符的情况较为常见,导致性能下降。
KMP算法:
通过构建部分匹配表(next数组)来优化字符匹配过程,避免了重复比较的开销。
该算法的时间复杂度为O(n+m),在处理长文本时表现出色,尤其适合模式串中存在大量重复前缀的情况。
KMP算法在匹配过程中利用已经匹配的信息,能够快速跳转到合适的位置,极大提高了匹配效率。
关键点:
部分匹配表:KMP算法的核心在于预处理模式串生成next数组,记录每个位置之前的最长相等前后缀的长度。这一信息使得在不匹配时能够迅速调整模式串的位置,而不是从头开始。
时间和空间复杂度:KMP算法在时间和空间复杂度上的优势使其成为处理字符串匹配问题的首选,尤其在需要频繁查找的场景中。
应用广泛:无论是在文本编辑器的查找功能、搜索引擎的关键词匹配,还是在数据挖掘中,KMP算法因其高效性和稳定性被广泛应用。



帖子还没人回复快来抢沙发