转载声明：文章来源https://blog.csdn.net/qq_38875964/article/details/134885610

概要

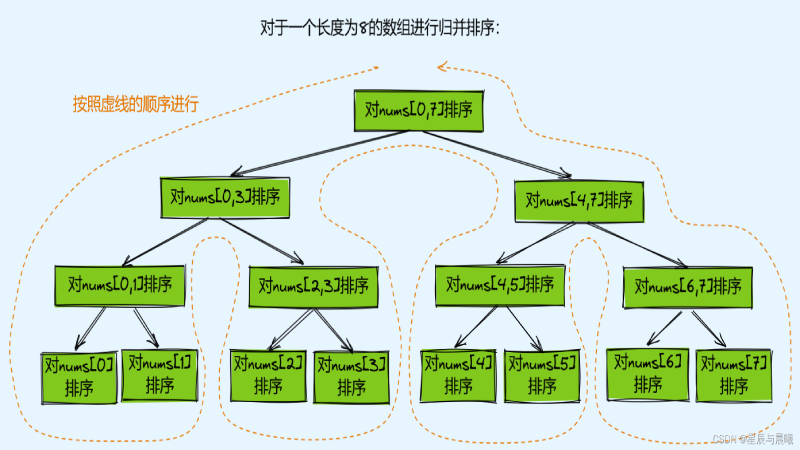
归并排序（Merge Sort）是应用分治思想的一个典型例子。把一个待排序序列拆分为两个子序列，分别对两个子序列排序，子序列排序时也采用相同的方法，直至拆分后的两个子序列都是有序的，即长度为1的序列天然有序，这时停止拆分，将两个有序的子序列归并为一个更大的有序序列，与之前拆分时的路径相反，不断的归并有序子序列，最终归并为一个序列。这种将两个有序序列归并为一个有序序列的操作称为二路归并。

二路归并：对比两个有序序列中最小的元素，也就是各自的第一个元素，其中更小的那个就是全局最小的元素，把它移到结果序列中，继续对比两个序列的首元素，得到全局第二小的元素，把它移到结果序列中，接下来的操作也是如法炮制，如此往复，直至其中一个序列为空，则可以把另一个序列剩下的元素直接并入结果序列，二路归并操作就算完成了。

自顶向下的归并排序

要对子数组 a[1o，hi)进行排序，先将它分为 a[1o，mid)和 a[mid，hi) 两部分，分别通过递归调用将它们单独排序，最后将有序的子数组归并为最终的排序结果。

自底向上的归并排序

想象每个元素都是长度为1的数组，将它们两两归并，得到很多组长度为2的有序数组，然后再四四归并，得到很多组长度为4的有序数组，再八八归并，如此这般，直至最后归为一个数组。

时间复杂度：O(nlogn)

空间复杂度：T(n)

Java实现代码

定义了一个排序接口，后面可用其它算法实现。

public interface Sort {
    void sort(int[] array);
    //交换数组i和j位置的值
    default void exchange(int[] array, int i, int j){
        int item = array[i];
        array[i] = array[j];
        array[j] = item;
    }
}

自顶向下的归并排序代码

/**
 * 归并排序
 */
public class MergeSort implements Sort{
    private int[] tem;
    @Override
    public void sort(int[] arr) {
        tem = new int[arr.length];
        merge_sort(arr,0,arr.length);
    }
    /**
     * 自顶向下的递归式归并排序
     */
    public void merge_sort(int[] arr, int lo, int hi) {
        if(hi - lo < 2){
            return;
        }
        int mid = (lo + hi)>>1;
        merge_sort(arr, lo, mid);
        merge_sort(arr, mid, hi);
        merge(arr,lo,mid,hi);
    }
    /**
     * 二路归并
     */
    public void merge(int[] arr, int lo, int mid, int hi){
        if(hi - lo == 1) return;
        int k = lo;
        while (k < hi){
            tem[k] = arr[k++];//备份
        }
 
        int i = lo;//左子数组的指针
        int j = mid;//右子数组的指针
        int p = lo;//结果数组的指针
        while (p < hi){//p移动到hi时说明归并完成
            if(i == mid)
                arr[p++] = tem[j++];
            else if(j == hi)
                arr[p++] = tem[i++];
            else if(tem[i] <= arr[j])
                arr[p++] = tem[i++];
            else
                arr[p++] = tem[j++];
        }
    }
 
    public static void main(String[] args) {
        MergeSort mergeSort = new MergeSort();
        TestUtil.test(10000,mergeSort);
    }
}

自底向上的归并排序代码

/**
     * 自底向上的归并排序
     */
    public void merge_sort(int[] arr){
        int length = arr.length;
        int len = 1;//子数组的大小
        while (len < length){
            for (int lo = 0; lo < length-len; lo += 2*len) {
                //数组末尾的右子数组长度可能不恰好是len
                merge(arr, lo, lo+len, Math.min(lo+2*len, length));
            }
            len = 2*len;//每趟遍历后子数组大小翻倍
        }
    }

 测试工具类，可生成测试数据和执行排序算法

public class TestUtil {
    /**
     * 返回一个大小为n的，由1到n之间的随机整数组成的数组
     */
    public static int[] getRandomArray(int n){
        return new Random().ints(n,1,n).toArray();
    }
 
    public void show(int array[]){
        System.out.println(Arrays.toString(array));
    }
 
    public static void test(int n,Sort sort) {
        int [] array = getRandomArray(n);
        long startTime = System.currentTimeMillis();
        sort.sort(array);
        long endTime = System.currentTimeMillis();
        //show(array);
        System.out.println("程序运行时间：" + (endTime - startTime) + "ms");
    }
}

用插入排序优化

用不同的方法处理小规模问题能改进大多数递归算法的性能，因为递归会使小规模问题中方法的调用过于频繁，所以改进对它们的处理方法就能改进整个算法。对排序来说，我们已经知道插入排序非常简单，因此很可能在小数组上比归并排序更快。当数组的长度小于某个值，比如15时，我们停止对其拆分，转而使用插入排序，一般可以将归并排序的运行时间缩短 10% ～ 15%，具体的改动也非常简单，只要稍微修改一下递归基的处理方式就可以了。

/**
     * 自顶向下的递归式归并排序
     */
    public void merge_sort(int[] arr, int lo, int hi) {
        if(hi - lo < 15){
            insertionSort(arr, lo, hi);
            return;
        }
        int mid = (lo + hi)>>1;
        merge_sort(arr, lo, mid);
        merge_sort(arr, mid, hi);
        merge(arr,lo,mid,hi);
    }
 
    /**
     * 插入排序
     */
    private void insertionSort(int[] array, int lo, int hi){
        int lef = lo;
        lo++;
        while(lo < hi){
            for(int i=lo;i>lef;i--){
                if(array[i] < array[i-1]){
                    exchange(array,i,i-1);
                }
            }
            lo++;
        }
    }

二路归并的一种优化

在备份辅助数组时只备份左子数组，右子数组在结果数组中不动，归并时元素先归并到结果数组的左边lo到mid的位置，当lo到mid的位置填满后，开始填入mid到hi，这时mid到hi也会因为归并时消耗了元素而恰好空出位置来，所以右子数组的元素不会被覆盖，这样能省下一半元素备份的时间。另外一点，当左子数组消耗完，即i==mid时，可以直接退出循环，不需要将右子数组剩余的元素并入结果数组，因为它们原本就在那里。

public void merge(int[] arr, int lo, int mid, int hi){
        if(hi - lo == 1) return;
        int k = lo;
        while (k < mid){
            tem[k] = arr[k++];//备份左子数组
        }
 
        int i = lo;//左子数组的指针
        int j = mid;//右子数组的指针
        int p = lo;//结果数组的指针
        while (p < hi){//p移动到hi时说明归并完成
            if(i == mid)
                break;//左子数组元素耗完直接退出
            else if(j == hi)
                arr[p++] = tem[i++];
            else if(tem[i] <= arr[j])
                arr[p++] = tem[i++];
            else
                arr[p++] = arr[j++];
        }

性能测试

分别测试了10^5，10^6，10^7，10^8数量级的排序时间
10^5：程序运行时间：11ms
10^6：程序运行时间：99ms
10^7：程序运行时间：1213ms
10^8：程序运行时间：11509ms
1亿规模数组的排序在我这个破电脑上也只要11秒，可见高效的算法对效率的提升。

应用场景

归并排序是一种高效稳定的排序算法，可用于大规模数据的排序，它的主要缺点是需要T(n)的辅助空间。