转载声明:文章来源https://blog.csdn.net/qq_40772692/article/details/80036959?ops_request_misc=&request_id=&biz_id=102&utm_term=%E5%AD%97%E7%AC%A6%E4%B8%B2KMP&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-3-80036959.142^v101^pc_search_result_base7&spm=1018.2226.3001.4187
一.KMP算法概述
1.KMP算法基本概念
KMP算法是一种高效的字符串匹配算法,算法名称取自于三位共同发明人名字的首字母组合。该算法的主要使用场景就是在字符串(也叫主串)中的模式串(也叫子串)定位问题,常见的有“求子串出现的起始位置”、“求子串的出现次数”等。
2.KMP算法核心
(1)朴素匹配算法
朴素匹配算法是一种暴力匹配的方式,其思想为依次枚举主串的每一个字符作为匹配模式串的起始字符,然后将两字符串的字符从起始位置一一比对,若在这个过程中出现某个字符不匹配,则将主串的起始比对位置重新回溯到上一个起始字符的下一位开始,模式串则回溯到第一个字符,重新开始匹配过程。直到子串字符全部匹配成功或主串枚举完仍匹配失败为止。整个算法的时间复杂度为 O(n*m) ,效率较低。


(2)KMP算法
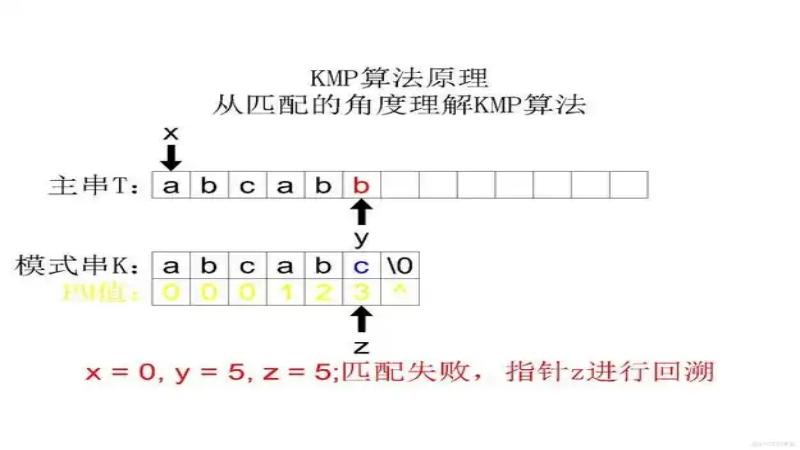
KMP算法对朴素匹配算法进行了改进,利用匹配失败时失败之前的已知部分时匹配的这个有效信息,保持主串的 i 指针不回溯,通过修改模式串(子串)的 j 指针,使模式串尽量地移动到有效的匹配位置。该算法的时间复杂度为 O(n+m),算法过程示例如下:


可以看到,在匹配失败时,我们不再按照朴素匹配算法的规则重新回溯主串指针和字串指针。而是保持主串指针不动,尽可能的移动子串指针到有效匹配位置。可以看出,这个子串最大有效匹配位置的特点如下:
匹配失败时:失败位置之前的主串(i前)和子串(j前)部分一定都是匹配的。且对于子串来说,失败位置之前(j前)的任一部分属于子串(模式串)的这段子串(子子串)的后缀
重新匹配时:我们重新匹配的开始一定是子串(模式串)的某部分前缀
要想移动子串(模式串)指针(i 下次匹配位置)到最大有效匹配位置,那么这个位置一定是这段前缀=后缀的部分
因此问题就转化为了如何求子串(模式串),在每一个字符位置处,以该字符为结尾的子子串的最大相等前缀和后缀的长度,我们将这个长度数组记录下为记为 next[] 。该数组一方面表示子串每个位置处的最大相等前后缀长度,另一方面也表示了在字符串匹配失败时,该位置使得模式串的回溯位置。
除此之外你可能会问:那我匹配失败时,有没有可能模式串的下次匹配位置不一定非得从这个后缀开始,有没有可能从前后缀的中间有一个相同的匹配段开始?答案是不可能,如果前后缀中间有一个相同的匹配段,那么这个段也一定属于后缀的一部分,因此模式串的下次最大有效匹配位置一定是看后缀的!(想一下就知道了,也可以自己推导一下)
说到这里,其实KMP算法的核心就可以总结为:充分利用匹配模式串的最大相同前后缀信息(子串本身的重复性),即利用next数组实现模式串的移动与回溯,而主串不回溯。减少匹配失败时的回溯次数,实现最大的移动量,从而提高匹配效率。(减少无意义的匹配)
3.KMP算法关系推导
该关系推导过程转自大佬 Kuangbin,辅助理解一下这个过程(看不懂也没关系),博客见 : ACM博客_kuangbin KMP算法
(1)推导前提
假设主串:S: S[1] S[2] S[3] ……S[n]
模式串:T: T[1] T[2] T[3]…..T[m]
现在我们假设主串第i 个字符与模式串的第j(j<=m)个字符‘失配’后,主串第i 个字符与模式串的第k(k<j)个字符继续比较,此时就有S[i] != T[j]
主串: S[1]...S[i-j+1]...S[i-1]S[i]...
||(匹配) || ≠
模式串: T[1]... T[j-1] T[j]
(2)由此,可以得到关系式如下:T[1]T[2]T[3]...T[j-1] = S[i-j+1]...S[i-1]
(3)由于S[i] != T[j],接下来S[i]将与T[k]继续比较,则模式串中的前k-1个字符串必须满足下列关系式,并且不可能存在k'>k满足下列关系式:
T[1]T[2]T[3]...T[k-1] = S[j-k+1]S[j-k+2]...S[i-1] (k<j)
(4)也就是说:
主串: S[1]...S[i-k+1]S[i-k+2]...S[i-1]S[i]...
|| || || ?(待比较)
模式串: T[1] T[2]... T[k-1] T[k]
(5)现在可以把前面的关系综合总结如下:
S[1]...S[i-j+1]...S[i-k+1]S[i-k+2]...S[i-1]S[i]...
|| || || || ≠
T[1]... T[j-k+1] T[j-k+2]... T[j-1] T[j]
|| || || ?
T[1] T[2] ... T[k-1] T[k]
现在唯一的任务就是如何求k了,通过一个next函数求。
二.next数组概述
1.next数组的含义
最长前缀概念: 最长前缀是说以第一个字符开始,但是不包含最后一个字符。
最长后缀概念: 最长后缀是说以最后一个字符开始,但是不包含第一个字符。
next 数组定义:在模式串中(下标从0开始),next[i] 表示模式串中以下标 i 处字符结尾的子串的最大相同前后缀的长度。在KMP算法中,该值一方面表示模式串中1~i位置子串中的最长相同前后缀长度,另一方面表示在该位置匹配失败时模式串回溯比较的下一个字符位置(最长前缀末座标的下一个字符)
2.如何求next数组
对于模式串 S 来说,首先初始化 next[0] = 0(一个字符不存在相同前后缀,所以长度为0)。假设在求取模式串 next 数组的过程中(与主串无关),已知 next[j] 现在要求 next[j+1] 则有以下两种情况:
若 S[ j+1 ] == S[ next[j] ] : 则 next[j+1] = next[j]+1;(next[j] 的值表示长度,但在下标为0开始的字符数组中就表示相等前缀末下标的下一位,因此不用+1即可)
若 S[ j+1 ] != S[ next[j] ] : 则说明该结尾处的相同前后缀应该比 j 处的更短一些,也就是我们要找一个更短的前缀和 j+1 处的后缀进行相等匹配。但是由 j 处的匹配可知 A~F 段的前后缀是相同的,因此这就等价于我们要在前缀 A~F 段中即 0~next[j]-1 中寻找一个尽可能大的相同前后缀。而之前的前后缀我们都已经求出了,于是比较就变成了 k = next[next[j] - 1] & S[j+1] == S[k] ?

总结如下:
令 next[0] = 0,假设next[j]=k, 即S[0...k-1] == S[j-k+1,j] ,则:
若S[j+1]==S[k] : next[j+1] = k+1
若S[j+1]!=S[k] : k = next[k-1] 重复此步骤,直到next[k]==0或匹配成功为止
三.KMP算法实现
1.古老版本(不好理解)
(1)next数组获取代码
int next[1000];
void getNext(string s,int l)//这里next是从0开始的,与字符串坐标一一对应,表示该0~下标处的最大长度。-1表示没有,0表示1,1表示2,以此类推!
{
next[0]=-1; //所以回溯的时候,回溯到的是最大前缀的末坐标k,而我们要比较的是k+1与j+1,所以坐标要后移一位于j+1比较,出现了s[k+1]
int k=-1; //但是next等于的还是最大后缀的末下标,与字符串下标对应。
for(int i=1;i<=l-1;i++)
{
while(k>-1&&s[k+1]!=s[i])
k=next[k];//回溯
if(s[k+1]==s[i])
k=k+1;//next[j+1]=next[j]+1;
next[i]=k;
}
}
int next[1000];
int getNext(char *s,int l)//这个版本,next数组是从1开始的,字符串是从0开始的,这里next 0就表示没有,数字表示长度
{
int j=0; //所以回溯的时候,回溯到的比如长度是2,在字符串里就是第三个字符,自动跳到了最大前缀末坐标的下一个,不用k+1了
int k=-1;
next[0]=-1;
while(j<l)
{
if(k==-1||s[j]==s[k])
next[++j]=++k;//next[j+1]=next[j]+1;
else
k=next[k];//回溯
}
}(2)KMP算法模板(求第一次出现位置+出现次数)
void getNext(string s,int l)
{
next[0]=-1;
int k=-1;
for(int i=1;i<=l-1;i++)
{
while(k>-1&&s[k+1]!=s[i])
k=next[k];
if(s[k+1]==s[i])
k=k+1;
next[i]=k;
}
}
int KMP(string s1,int l1,string s2,int l2)
{
int k=-1;
for(int i=0;i<l1;i++)
{
while(k>-1&&s2[k+1]!=s1[i])
k=next[k];
if(s2[k+1]==s1[i])
k=k+1;
if(k==l2-1)
return i-l2+1;
}
return -1;
}
void KMP(char *str,int l1,char *s,int l2)
{
int k=-1;
for(int i=0;i<l1;i++)
{
while(k>-1&&s[k+1]!=str[i])
k=next[k];
if(s[k+1]==str[i])
k=k+1;
if(k==l2-1)
{
sum++;
k=next[k];
}
}
}2.清晰版本
(1)next数组获取代码
void getNext(char* s,int len){
next[0] = 0;
int k = 0; //k = next[0]
int i = 1;
while(i < len){
if(s[i] == s[k]){
next[i++] = ++k; //next[j+1] = k+1;
}else{
if(k > 0)k = next[k-1]; //k = next[k-1]
else{
next[i++] = k; //next[j+1] = 0 回溯到头了,找不到相同前缀,则最大相同前后缀长度=0
}
}
}
}
void getNext(char* s,int len){
next[0] = 0;
int k = 0; //k = next[0]
for(int i = 1;i < len;i++){
while(k > 0 && s[i] != s[k])k = next[k-1]; //k = next[k-1]
if(s[i] == s[k])k++;
next[i] = k; //next[j+1] = k+1 | next[j+1] = 0
}
}(2)KMP算法模板
//返回模式串T中字串S第一次出现的位置下标,找不到则返回-1
int kmp(char *T, char* S){
int len_T = strlen(T);
int len_S = strlen(S);
for(int i = 0,j = 0;i<len_T;i++){
while(j > 0 && T[i] != S[j])j = next[j-1];
if(T[i] == S[j])j++;
if(j == len_S)return i-len_S+1;
}
return -1;
}
//返回模式串T中字串S出现的次数,找不到则返回0
int kmp(char *T, char* S){
int sum = 0;
int len_T = strlen(T);
int len_S = strlen(S);
for(int i = 0,j = 0;i<len_T;i++){
while(j > 0 && T[i] != S[j])j = next[j-1];
if(T[i] == S[j])j++;
if(j == len_S){
sum++;
j = next[j-1];
}
}
return sum;
}


帖子还没人回复快来抢沙发