转载声明：文章来源https://blog.csdn.net/m0_56911648/article/details/130856402

（1）基本思想

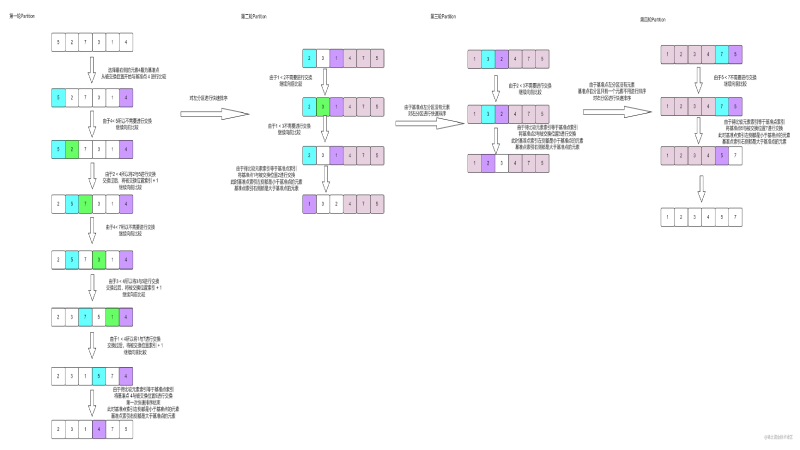
任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

（2）代码实现

1) 挖坑法

划分完之后，再左右递归。当遇到array[right] >= tmp ，交换 array[left] 和 array[right] ；

以此类推，最终得到正确排序。

public static int partition(int[] array,int left,int right){
        int tmp =array[left];
        while (left < right) {
            while (left < right && array[right] >= tmp){
                right--;
            }
            array[left] = array[right];
            while (left < right && array[left] <= tmp){
                left++;
            }
            array[right] = array[left];
        }
        array[left] = tmp;
        return left;
    }
    public static void quickSort(int[] array) {
        quick(array,0,array.length-1);
    }
    public static void quick(int[] array,int start,int end) {
        if (start >= end) {
            return;
        }
        //先划分，再左右递归
        int pivot = partition(array,start,end);
        quick(array,start,pivot-1);
        quick(array,pivot+1,end);
    }

2）Hoare法

当 right 找到比基准小的 ，left 找到比基准大的时 交换它们的值。

public static int partition2(int[] array,int left,int right){
        int tmp =array[left];
        int i = left;
        while (left < right) {
            while (left < right && array[right] >= tmp){
                right--;
            }
            while (left < right && array[left] <= tmp){
                left++;
            }
            swap(array,left,right);
        }
        //相遇之后
        swap(array,left,i);
        return left;
 }

swap 方法为交换方法，在我前面的文章中写过，这里就不写了，有需要的可以翻一下上一篇文章。

3）前后指针法（了解即可）

写法1：

private static int partition(int[] array, int left, int right) {
int prev = left ;
int cur = left+1;
while (cur <= right) {
if(array[cur] < array[left] && array[++prev] != array[cur]) {
swap(array,cur,prev);
}
cur++;
}
swap(array,prev,left);
return prev;
}

写法2：

private static int partition(int[] array, int left, int right) {
int d = left + 1;
int pivot = array[left];
for (int i = left + 1; i <= right; i++) {
if (array[i] < pivot) {
swap(array, i, d);
d++;
}
}
swap(array, d - 1, left);
return d - 1;
}

4）非递归实现快速排序

public static void quickSort(int[] array) {
        Deque<Integer> stack = new LinkedList<>();
        int left = 0;
        int right = array.length-1;
        int pivot = partition(array,left,right);
        if (pivot > left+1) {
            stack.push(left);
            stack.push(pivot-1);
        }
        if (pivot < right-1) {
            stack.push(pivot+1);
            stack.push(right);
        }
        while (!stack.isEmpty()) {
            right = stack.pop();
            left = stack.pop();
            pivot = partition(array,left,right);
            if (pivot > left+1) {
                stack.push(left);
                stack.push(pivot-1);
            }
            if (pivot < right-1) {
                stack.push(pivot+1);
                stack.push(right);
            }
        }
    }

（3）特性总结

1. 快速排序整体的综合性能和使用场景都是比较好；

2. 时间复杂度：O(N*logN） 空间复杂度：O(logN)；

3.稳定性：不稳定。

（4）快速排序的优化

当需要排序的元素太多，我们这时选取基准就非常重要了，因此我们采取三数取中法来选取合适的基准。

三数取中法：在三个数当中选出既不是最大的也不是最小的。

private static int midTree(int[] array,int left,int right) {
        int mid = (left+right)/2;
        if (array[left] < array[right]) {
            if (array[mid] < array[left]) {
                return left;
            } else if(array[mid] > array[right]) {
                return right;
            } else {
                return mid;
            }
        } else {
            if (array[mid] < array[right]) {
                return right;
            } else if(array[mid] > array[left]) {
                return left;
            } else {
                return mid;
            }
        }
    }